Definition of Symmetric relation
What is the definition of Symmetric relation?
Here we will explain the symmetric relation on set.
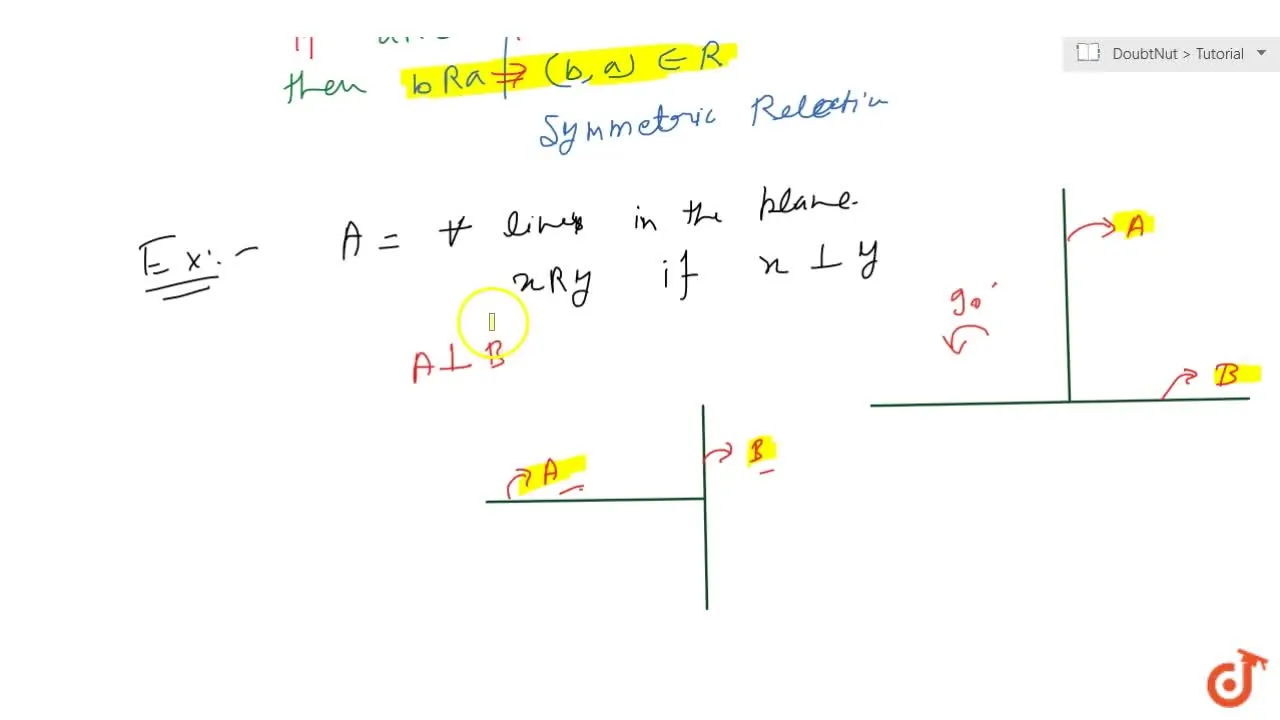
Let A be a set where the relation R is defined. Here, R is said to be a symmetric relation, if (a, b) ∈ R ⇒ (b, a) ∈ R. So, aRb ⇒ bRa for all (a, b) ∈ R.
If we consider the set A of natural numbers and if there is a relation A that is defined by “x + y = 5”, then this relation is symmetric in A, for
a + b = 5 ⇒ b + a = 5
At the same time in case of the set A of natural numbers if the relation R is defined as ‘x is a divisor of y’, then the relation R cannot be symmetric as 3R9 does not imply 9R3. It is because 3 divides 9, but 9 does not divide 3.
For a symmetric relation R, R−1−1= R.
Solved examples on symmetric relation on set
1. A relation R is defined on the set Z by “a R b if a – b is divisible by 5” for a, b ∈ Z. Find out if R is a symmetric relation on Z.
Solution:
Let a, b ∈ Z and aRb hold. Here, a – b is divisible by 5 and so b – a is divisible by 5.
So, it can be found that aRb ⇒ bRa. Therefore R is symmetric.
2. A relation R is defined on the set Z (set of all integers) by “aRb if and only if 2a + 3b is divisible by 5”, for all a, b ∈ Z. Find out if R is a symmetric relation on Z.
Solution:
Let a, b ∈ Z and aRb holds i.e., 2a + 3a = 5a, which is divisible by 5. Now, 2a + 3a = 5a – 2a + 5b – 3b = 5(a + b) – (2a + 3b) is also divisible by 5.
So, here aRa holds for all a in Z. Therefore R is reflexive.
3. Let R be a relation on Q which is defined by R = {(a, b) : a, b ∈ Q and a – b ∈ Z}. Prove that R is Symmetric relation.
Solution:
Given R = {(a, b) : a, b ∈ Q, and a – b ∈ Z}.
Let ab ∈ R ⇒ (a – b) ∈ Z, i.e. (a – b) is an integer.
⇒ -(a – b) is an integer
⇒ (b – a) is an integer
⇒ (b, a) ∈ R
Here (a, b) ∈ R ⇒ (b, a) ∈ R
Therefore, R is symmetric.
4. Let m is fixed positive integer.
Let R = {(a, a) : a, b ∈ Z and (a – b) is divisible by m}.
Prove that R is symmetric relation.
Solution:
Given R = {(a, b) : a, b ∈ Z, and (a – b) is divisible by m}.
Let ab ∈ R . Then,
ab ∈ R ⇒ (a – b) is divisible by m
⇒ -(a – b) is divisible by m
⇒ (b – a) is divisible by m
⇒ (b, a) ∈ R
Here, (a, b) ∈ R ⇒ (b, a) ∈ R
Thus, R is symmetric relation on set Z.
Similar Questions
Consider the following statements
1. Identify , relation in a finite set A is the greatest relation in A.
2. The universal relation in a set containing at least 2 elements is non anti symmetric
3. The union and intersection of two symmetric relations are also symmetric relations.
Whcih of these is/are correct?View SolutionDefinition of Reflexive relation
View SolutionDefine a symmetric relation.
View SolutionDefinition of Transitive relation
View SolutionLet M be the set of men and R is a relation "is son of" defined on M. Then, R is (a) an equivalence relation (b) a symmetric relation (c) a transitive relation (d) None of these
View SolutionLet M be the set of men and R is a relation 'is son of defined on M. Then, R is (a) an equivalence relation (b) a symmetric relation only (c) a transitive relation only (d) None of the above
View SolutionIf a relation R in N defined as R=((a,b):a<b, for every a,b∈N) then R is
(A) Only transitive relation.
(B) Only symmetric relation.
(C) Only reflexive relation.
(D) Transitive and symmetric relation.View SolutionIf A={1,2,3}, the number of symmetric relations in A is
View SolutionWhat is the adequate definition of language relation preestimation:
View SolutionIf the set A has 10 elements, then the ratio of total number of reflexive relations to total number of symmetric relations is 2k then k=
View Solution