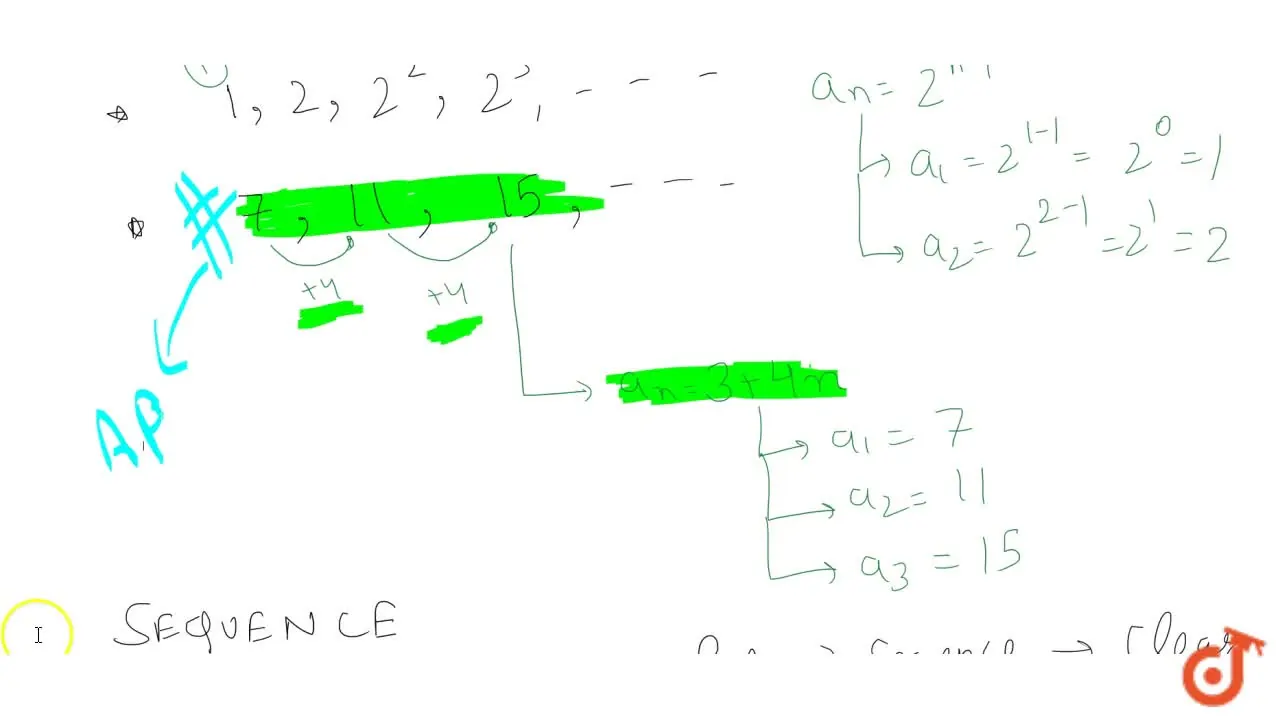
Definition of Sequence with example .
Video Solution
|
Answer
Step by step video, text & image solution for Definition of Sequence with example . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023
Similar Questions
Definitions
View SolutionDefinitions
View SolutionDefinitions
View SolutionDefinition and example
View SolutionExplain the law of definite proportions with an example.
View SolutionDefinition with examples
View SolutionDefinition OF sequence and progression||Imp. points and Illustration
View Solutiondefinitions Nutrients :
View SolutionTypes of Subsets (definition with examples)
View SolutionGive definitions of following along with examples.
(a) Calcination
(b) RoastingView Solution