Cuboid
Cuboid
In this chapter, you would be able to get the best idea on cuboid as well as cuboid formula volume. We would also include the study of the surface area of a cuboid. To make things clearer, we will work on some solved problems.
What is cuboid?
A cuboid is a three-dimensional shape that consists of eight vertices, six faces, and twelve edges. In other words, it is a polyhedron where the faces of the cuboid are parallel as well as equal in dimensions. Compared to the cube and cylinders, the area and volume differ.
What is the shape of a cuboid?
A cuboid is bounded by six rectangular plane reasons which are a closed 3-dimensional geometrical figure.
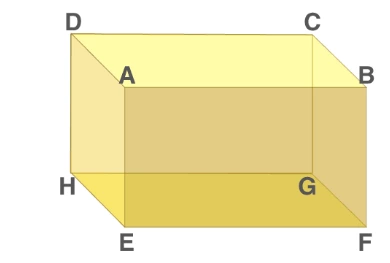
Cuboid formula
Have a look at the cuboid below where the breadth is ‘b’ cm, length be ‘l’ cm and height be ‘h’ cm.
So, here,
Area of face BFGC = Area of face AEHD = (b ×h) cm2
Area of face EFGH = Area of Face ABCD = (l× b) cm2
Area of face DHGC = Area of face ABFE = (l ×h) cm2
Here, Total surface area of a cuboid = Sum of the areas of all its 6 rectangular faces
In other words, Total Surface Area of a Cuboid = 2 (lb + bh + lh )
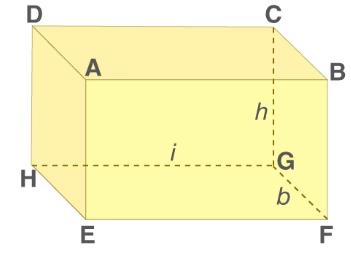
Lateral surface area of a Cuboid
The lateral surface area of a solid is the sum of surface areas of all sides except the top and bottom face of solid
Let us consider a Cuboid of length to be ‘l’, breadth to be ‘b’ and height to be ‘h’.
Now, the lateral surface area of the cuboid= Area of face ADHE + Area of face ABFE + Area of face BCGF + Area of face DCGH
=2 (b × h) + 2 (l × h)
=2h (l + b)
So Lateral Surface of a Cuboid = 2h ( l + b )
Volume of Cuboid
The cuboid volume is equal to the product of the area of one surface and height.
So, Volume of the Cuboid = ( l x b x h) cubic units.
Diagonal of cuboid
It is important to note that the length of diagonal of the cuboid is √( l2 + b2 +h2)
Perimeter of Cuboid
It on the basis of the length, width and height, that the perimeter of the cuboid is calculated. The value of the edges is different because the cuboid has 12 edges. So, the perimeter is:
Perimeter of a cuboid = 4 (l + b + h)
Here, l, b and h are length, breadth and height, respectively.
Now, we will summarize all the formulas in the table below:
Formulas
Cuboid
Surface Area
2(lb + bh +lh)
Lateral Surface Area
2h(l +b)
Volume
l × b × h
Diagonal Length
√( l2 + b2 +h2)
Perimeter
4 (l + b + h)
Related Videos:
- Volume of a cuboid
- Surface area of a cuboid
- Cube and Solid cube
- Lateral surface area of a cuboid
- Surface area of cube
- Lateral surface area of cube
We will now proceed further to solve different problems on cuboid to get a clear understanding of it.
Problem 1: A cuboid has dimensions of 3 inches × 4 inches × 4 inches. Find the total surface area?
Solution: Here,
Length = 3 inches
Breadth = 4 inches
Height = 4 inches
We know that the total Surface Area (TSA) = 2 (lb + bh + hl )
TSA = 2 (3 ×4 + 4 × 7 + 4 × 3)
TSA = 2 (12 + 28 + 12)
TSA = 104
So, we find that the total surface area of this cuboid is 104 inches2
Problem 2: A cuboid has dimensions of 4 inches × 5 inches × 7 inches. Calculate the total surface area?
Solution: Here,
Length = 4 inches
Breadth = 5 inches
Height = 7 inches
We know that the total Surface Area (TSA) = 2 (lb + bh + hl )
TSA = 2 (4 × 5 + 5 × 7 + 7 × 4)
TSA = 2 (20 + 35 + 28)
TSA = 166
So, we find that the total surface area of this cuboid is 166 inches2
Problem 3: The length, width and height of a cuboid are 10 cm, 12 cm and 15 cm respectively. Find the lateral surface area of the cuboid?
Solution: Given,
Length = 10 cm
Breadth = 12 cm
Height = 15 cm
As we know
Lateral surface area of a cuboid is:
LSA = 2h ( l + w )
So, LSA = 2 × 15 (10 + 12)
LSA = 660 cm2
Problem 4: A cube has its sides equal to 4 cm in length. Find the surface area of it.
Solution: Given length, ‘a’= 4 cm
Surface area of the cube = 6a2
= 6× 42
= 6 ×16
= 96 cm2
Important Chapters:


Formulas
Cuboid
Surface Area
2(lb + bh +lh)
Lateral Surface Area
2h(l +b)
Volume
l × b × h
Diagonal Length
√( l2 + b2 +h2)
Perimeter
4 (l + b + h)
