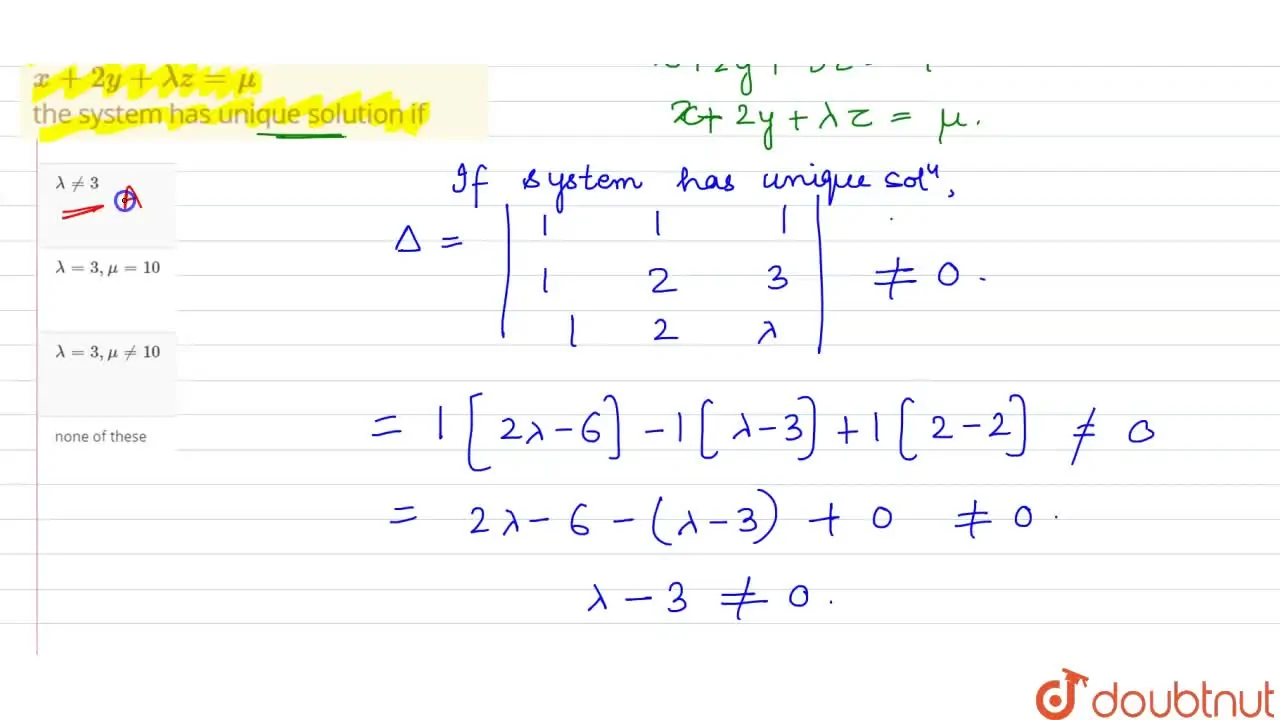Consider the system of equations
x+y+z=6
x+2y+3z=10
x+2y+λz=μ
the system has unique solution if
λ≠3
λ=3,μ=10
λ=3,μ≠10
none of these
The correct Answer is:A
Δ=∣∣
∣∣11112312λ∣∣
∣∣=2λ+3+2−2−λ−6=λ−3
Δ1=∣∣
∣
∣∣6111023μ2λ∣∣
∣
∣∣=12λ+3μ+20−2μ−10λ−36
=2λ+μ−16
Δ2=∣∣
∣
∣∣16111031μλ∣∣
∣
∣∣=10λ+18+μ−10−3μ−6λ=4λ−2μ+8
Δ3=∣∣
∣
∣∣116121012μ∣∣
∣
∣∣=2μ+10+12−12−μ−20=μ−10
Thus the system has unique solutions if Δ≠0 or λ≠3 and the system has infinite solution if Δ=Δ1=Δ2=Δ3=0 ot λ=3 and μ=10. System has no solution if Δ=0 and at least one of Δ1,Δ2,Δ3 is nonzero of λ=3 and μ≠=10
Similar Questions
Consider the system of equations
x+y+z=6
x+2y+3z=10
x+2y+λz=μ
The system has no solution ifView SolutionConsider the system of equations
x+y+z=6
x+2y+3z=10
x+2y+λz=μ
the system has infinite solutions ifView SolutionIf the system of linear equations x+y+z=6, x+2y+3z=14 and 2x +5y+λz=μ(λ,μ≠R) has a unique solution if λ is
View SolutionThe system of equations x+y+z=6,x+2y+3z=10,x+2y+λz=μ has no solution for
View SolutionThe system of equations x−y+3z=4,x+z=2 x+y−z=0 has
View SolutionConsider the system of equation x+y+z=6,x+2y+3z=10,andx+2y+λz=μ. Statement 1: if the system has infinite number of solutions, then μ=10. Statement 2: The determinant |116121012μ|=0forμ=10.
View SolutionConsider the system of equation x+2y−3z=a,2x+6y−11z=b,x−2y+7c then
View SolutionConsider the system of equations
x+y+z=5, x+2y+3z=9, x+3y+λz=μ
The sustem is called smart brilliant good and lazy according as it has solution unique solution infinitely many solution respectively .
The system is smart ifView SolutionConsider the system of equations
x+y+z=5, x+2y+3z=9, x+3y+λz=μ
The sustem is called smart brilliant good and lazy according as it has solution unique solution infinitely many solution respectively .
The system is good ifView SolutionConsider the system of equations
x+y+z=5, x+2y+3z=9, x+3y+λz=μ
The sustem is called smart brilliant good and lazy according as it has solution unique solution infinitely many solution respectively .
The system is lazy ifView Solution