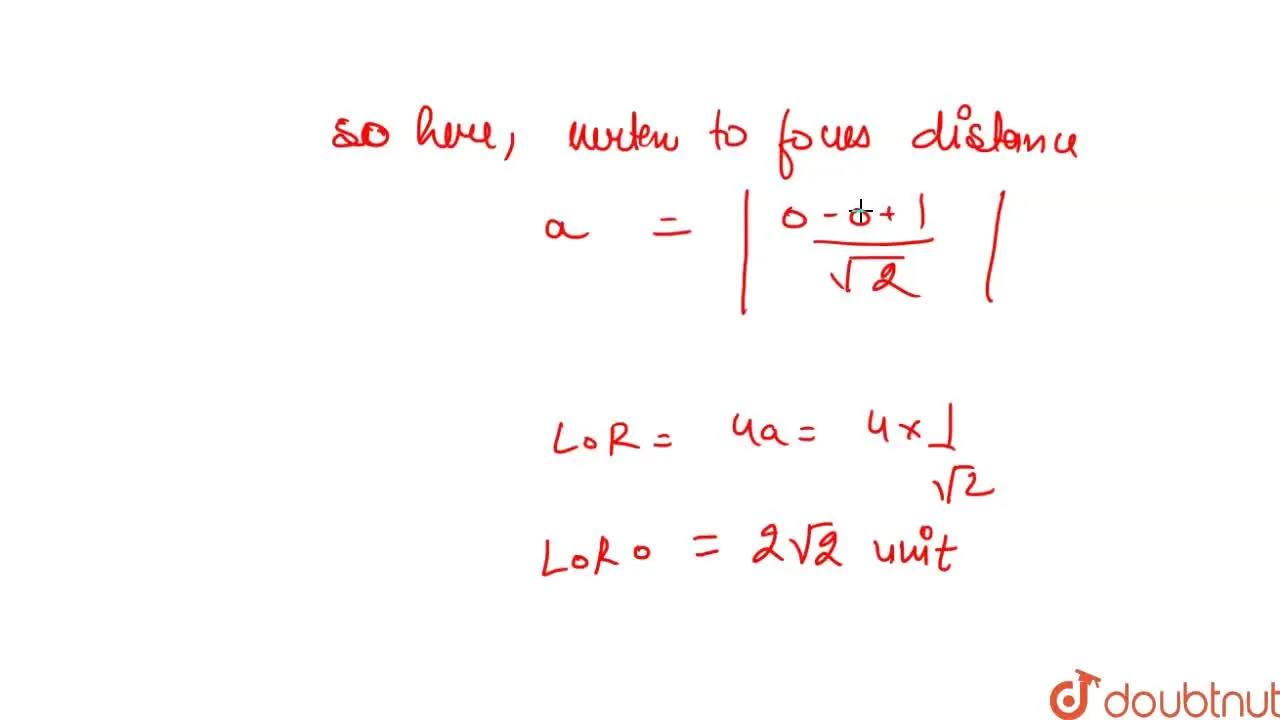Consider the parabola whose focus is at (0,0) and tangent at vertex is x-y+1=0
The length of latus rectum is
4√2
2√2
8√2
3√2
The correct Answer is:B
(2)

The distance between the focus and tangent at the vertex is
|0−0+1|√12+12=1√2
The directrix is the line parallel to the tangent vertex ant at a distance 2×1√2 from the focus.
Let the equation of the directrix be
x−y+λ=0
where λ√12+12=2√2
∴ λ=2
Let P (x,y) be any moving point on the parabola. Then, OP=PM
orx2+y2=(x−y+2√12+1)2
or2x2+=2y2=(x−y+2)2
orx2+y2+2xy−4x+4y−4=0
Latus rectum length =2× (Distance of focus from directrix)
2∣∣
∣∣0−0+2√12+12∣∣
∣∣=2√2
Solving the parabola with the x-axis, we get
x2−4x−4=0
orx=4±√322=2±2√2
Therefore, the length of chord on the x-axis is 4√2.
Since the chord 3x+2y=0 passes through the focus, it is focus chord.
Hence, tangents at the extremities of chord are perpendicular.
Related Playlists
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Matrix)4videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Numerical)28videos
PARABOLA
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Multiple)26videos
PARABOLA
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank19videos
PERMUTATION AND COMBINATION
Similar Questions
Consider the parabola whose focus is at (0,0) and tangent at vertex is x-y+1=0
The length of the chord of parabola on the x-axis isView SolutionConsider the parabola whose focus is at (0,0) and tangent at vertex is x-y+1=0
Tangents drawn to the parabola at the extremities of the chord 3x+2y=0 intersect at angleView SolutionConsider the parabola whose focus is at (0,0) and tangent at vertex is x-y+1=0
Tangents drawn to the parabola at the extremities of the chord 3x+2y=0 intersect at angleView SolutionThe equation of directrix of a parabola is 3x+4y+15=0 and equation of tangent at vertex is 3x+4y−5=0,Then the length of latus rectum is equal to
View SolutionProve that the equation of the parabola whose focus is (0, 0) and tangent at the vertex is x−y+1=0is x2+y2+2xy−4x+4y−4=0.
View Solutionthe equation of the parabola whose focus is the point (0,0) and the tangent at the vertix is x−y+1=0 is
View Solutionthe equation of the parabola whose focus is the point (0,0) and the tangent at the vertix is x−y+1=0 is
View SolutionLet y=3x-8 be the equation of the tangent at the point (7, 13 ) lying on a parabola whose focus is at (-1,-1). Find the equation of directrix and the length of the latus rectum of the parabola.
View SolutionFind the equation of the parabola whose focus is (3,0) and vertex is (0,0).
View SolutionThe equation of latus rectum of a parabola is x+y=8 and cquation of the tangent at the vertex is x+y=12. Then the length of latus rectum is
View Solution