Consider the graphs ofy=Ax2andy2+3=x2+4y, where A is a positive constant and x,y∈R.Number of points in which the two graphs intersect, is
The correct Answer is:4
To find the number of points of intersection between the graphs of y=Ax2 and y2+3=x2+4y, we can follow these steps:
Step 1: Rewrite the second equation
The second equation is given as:
y2+3=x2+4y
Rearranging this gives:
y2−4y+3=x2
Step 2: Factor the quadratic in y
The left-hand side can be factored:
(y−2)2−1=x2
This simplifies to:
(y−2)2=x2+1
Step 3: Recognize the hyperbola
The equation (y−2)2−x2=1 is the standard form of a hyperbola centered at (0,2) with a vertical transverse axis.
Step 4: Substitute the parabola equation
Now substitute y=Ax2 into the hyperbola equation:
(Ax2−2)2−x2=1
Step 5: Expand and simplify
Expanding the left-hand side:
(A2x4−4Ax2+4)−x2=1
This simplifies to:
A2x4−(4A+1)x2+3=0
Step 6: Let z=x2
Let z=x2. Then, the equation becomes:
A2z2−(4A+1)z+3=0
Step 7: Use the discriminant to find the number of solutions
The number of points of intersection depends on the discriminant of this quadratic equation. The discriminant D is given by:
D=(4A+1)2−4⋅A2⋅3
Calculating this gives:
D=(4A+1)2−12A2
Expanding:
D=16A2+8A+1−12A2=4A2+8A+1
Step 8: Analyze the discriminant
The discriminant D=4A2+8A+1 is a quadratic in A and since the coefficient of A2 is positive, it opens upwards. The discriminant is always positive for all A>0.
Step 9: Conclusion on the number of intersections
Since the discriminant is positive, there are two distinct real solutions for z, which means there are two values of x2. Each value of x2 corresponds to two values of y (since y=Ax2 is a function of x2). Therefore, the total number of intersection points is:
2×2=4
Thus, the number of points in which the two graphs intersect is 4.
---
The second equation is given as:
y2+3=x2+4y
Rearranging this gives:
y2−4y+3=x2
The left-hand side can be factored:
(y−2)2−1=x2
This simplifies to:
(y−2)2=x2+1
The equation (y−2)2−x2=1 is the standard form of a hyperbola centered at (0,2) with a vertical transverse axis.
Now substitute y=Ax2 into the hyperbola equation:
(Ax2−2)2−x2=1
Expanding the left-hand side:
(A2x4−4Ax2+4)−x2=1
This simplifies to:
A2x4−(4A+1)x2+3=0
Let z=x2. Then, the equation becomes:
A2z2−(4A+1)z+3=0
The number of points of intersection depends on the discriminant of this quadratic equation. The discriminant D is given by:
D=(4A+1)2−4⋅A2⋅3
Calculating this gives:
D=(4A+1)2−12A2
Expanding:
D=16A2+8A+1−12A2=4A2+8A+1
The discriminant D=4A2+8A+1 is a quadratic in A and since the coefficient of A2 is positive, it opens upwards. The discriminant is always positive for all A>0.
Since the discriminant is positive, there are two distinct real solutions for z, which means there are two values of x2. Each value of x2 corresponds to two values of y (since y=Ax2 is a function of x2). Therefore, the total number of intersection points is:
2×2=4
Topper's Solved these Questions
- HYPERBOLABook:CENGAGE ENGLISHChapter:HYPERBOLAExercise:JEE MAIN
Explore 3 Videos
- HYPERBOLABook:CENGAGE ENGLISHChapter:HYPERBOLAExercise:JEE ADVANCED
Explore 6 Videos
- HYPERBOLABook:CENGAGE ENGLISHChapter:HYPERBOLAExercise:MATRIX MATHC TYPE
Explore 10 Videos
- HIGHT AND DISTANCE Book:CENGAGE ENGLISHChapter:HIGHT AND DISTANCE Exercise:Archives
Explore 3 Videos
- INDEFINITE INTEGRATIONBook:CENGAGE ENGLISHChapter:INDEFINITE INTEGRATIONExercise:Multiple Correct Answer Type
Explore 2 Videos
Similar Questions
Knowledge Check
Which is the graph of y=−(x−2)2 ?
A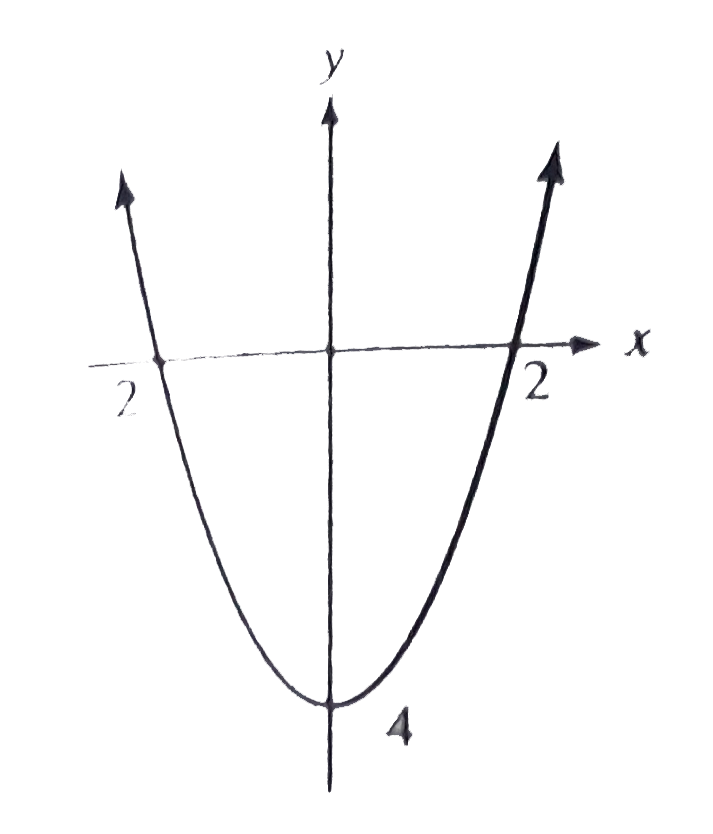 B
B C
C D
D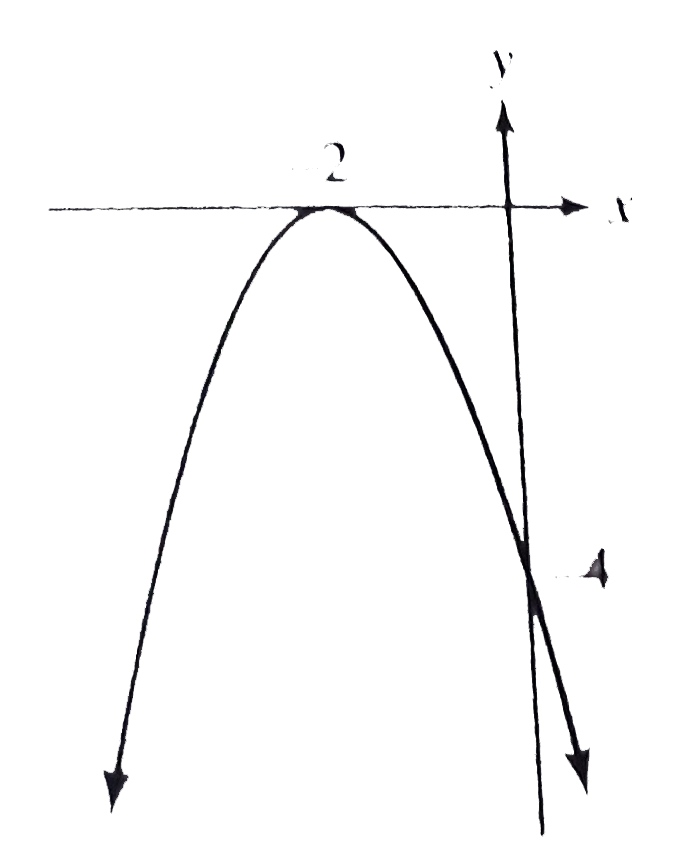
The graph of x2=(2y+3)2 is
Aan ellipseBa parabolaCa hyperbolaDintersecting linesThe graphs of y=2x-5 and x + 3y=-1 intersect at
A(-1,2)B(-2,-1)C(2,-1)D(-2,1)
Draw the graph of y=2x3−15x2+36x+12 y=−x4+2x2−3
View SolutionProve that graphs of y=x2+2andy=3x−4 never intersect.
View SolutionConsider the two graphs y=2x and x2−xy+2y2=28. The absolute value of the tangent of the angle between the two curves at the points where they meet, is ……………
View SolutionFind the points at which the graphs of y=12x2−3 and y=x +1 intersect.
View SolutionThe graph of y=log5xandy=ln 0.5x intersect at a point where x equals
View Solution

