Consider the following propositions :
P : I take medicine , q : I can sleep
Then , the compound statement ~p→~q means
If I do not take medicine, then I cannot sleep
If I do not take medicine, then I can sleep
I take medicine iff can sleep
I take medicine if I can sleep
The correct Answer is:A
To solve the problem, we need to analyze the given propositions and the compound statement.
1. Identify the propositions:
- Let P represent "I take medicine."
- Let Q represent "I can sleep."
2. Negate the propositions:
- The negation of P (denoted as ∼P) is "I do not take medicine."
- The negation of Q (denoted as ∼Q) is "I do not sleep."
3. Understand the compound statement:
- The compound statement given is ∼P→∼Q. This can be read as "If I do not take medicine, then I cannot sleep."
4. Interpret the statement:
- The statement ∼P→∼Q indicates a conditional relationship. It suggests that the lack of taking medicine (not taking medicine) leads to the inability to sleep (not being able to sleep).
5. Conclusion:
- Therefore, the compound statement ∼P→∼Q means "If I do not take medicine, then I cannot sleep."
Final Answer:
The compound statement ∼P→∼Q means "If I do not take medicine, then I cannot sleep."
- Let P represent "I take medicine."
- Let Q represent "I can sleep."
- The negation of P (denoted as ∼P) is "I do not take medicine."
- The negation of Q (denoted as ∼Q) is "I do not sleep."
- The compound statement given is ∼P→∼Q. This can be read as "If I do not take medicine, then I cannot sleep."
- The statement ∼P→∼Q indicates a conditional relationship. It suggests that the lack of taking medicine (not taking medicine) leads to the inability to sleep (not being able to sleep).
- Therefore, the compound statement ∼P→∼Q means "If I do not take medicine, then I cannot sleep."
The compound statement ∼P→∼Q means "If I do not take medicine, then I cannot sleep."
Topper's Solved these Questions
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMA ENGLISHChapter:MATHEMATICAL REASONING Exercise:Solved MCQs
Explore 5 Videos
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMA ENGLISHChapter:MATHEMATICAL REASONING Exercise:Section II - Assertion Reason Type
Explore 3 Videos
- MATHEMATICAL REASONING Book:OBJECTIVE RD SHARMA ENGLISHChapter:MATHEMATICAL REASONING Exercise:illusration 3
Explore 1 Video
- MATHEMATICAL INDUCTION Book:OBJECTIVE RD SHARMA ENGLISHChapter:MATHEMATICAL INDUCTION Exercise:Exercise
Explore 30 Videos
- MAXIMA AND MINIMA Book:OBJECTIVE RD SHARMA ENGLISHChapter:MAXIMA AND MINIMA Exercise:Chapter Test
Explore 29 Videos
Similar Questions
Consider the following propositions :
P : It rains ,q : Then street gets flooded.
the propostion " If it does not rain, then the street not get flooded," is represented by
View SolutionConsider the following propositions
p : it rains , q : The street gets flooded.
The proposition " If it does not rain, then the street does not get flooded" is represented by
View SolutionConsider the following statements
P : I have the raincoat q : I can walk in the rain.
The propositions " If i have the raincoat , then I can walk in the rain " is represented by
View SolutionConsider the following reaction sequence

The compounds P and Q are :
View SolutionLet p and q be two propositions given by
p : I play cricket during the holidays.
q : I just sleep throughout the day.
Then, the compound statement p∨q is
View SolutionConsider the following reaction , the compounds P and Q are respectively
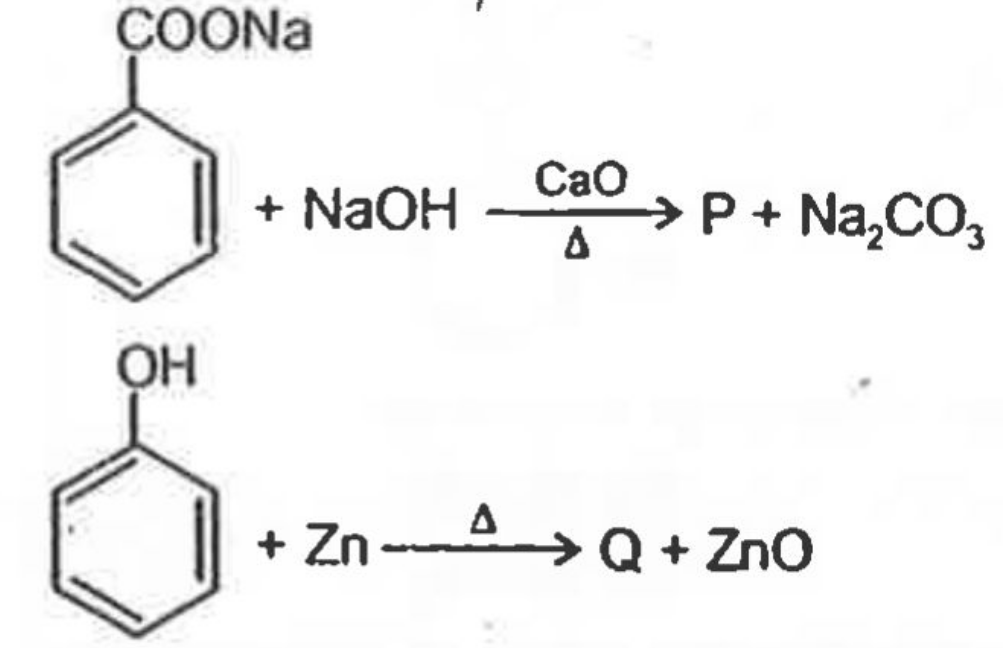
View SolutionThe proposition p→~(p∧~q) is
View SolutionWhich of the following is true for the propositions p and q ?
View SolutionThe logical statement (p→q)∨(q→~p) is :
View SolutionConsider the following statements:
p : I shall pass, q : I study
The symbolic represention of the proposition " I shall pass iff I study" is
View Solution

