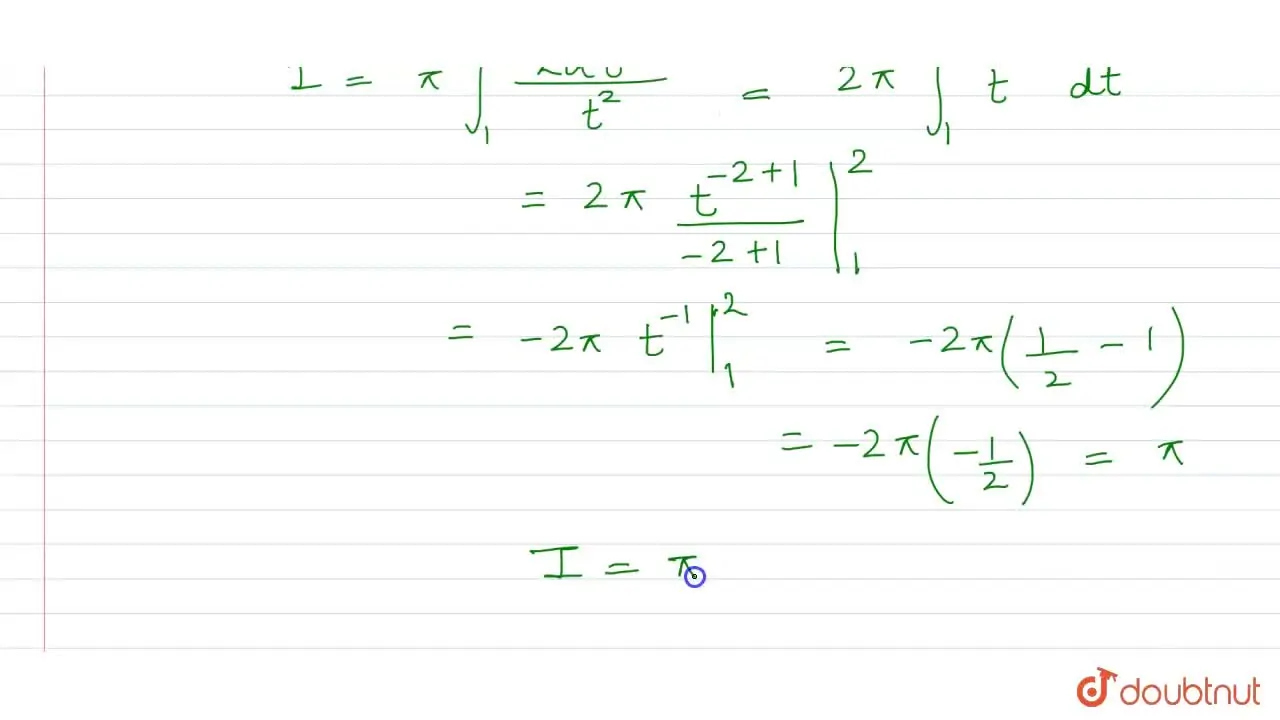Consider I=∫π0xdx1+sinx
What is I equal to ?
A
π
B
0
C
π
D
2π
Video Solution
Text Solution
The correct Answer is:C
Given , I=∫π0xdx1+sinx…….(i)
=∫π0(π−x)1+sin(π−x)dx
[∵∫0f(x)dx=∫a0f(a−x)dx]
=∫π0(π−x)1+sinxdx……..(ii)
[∵sin(π−x)=sinx]
Adding eqs. (i) and (ii) , we get
2I=π∫π0dx1+sinx.........(iii)
⇒2I=2π∫π20dx1+sinx
[∵∫2a0f(x)dx=2∫a0f(x)dx if f(2a−x)=f(x)]
⇒I=π∫π20dx1+(2tan'x21+tan2'x2)
⇒I=π∫π20sec2'x2dxtan2'x2+1+2tan'x2
=I=π∫π20(sec2'x2)(tan'x2+1)2
Let tan'x2+1=t
⇒sec2'x2.12dx=dt
⇒sec2'x2dx=2dt
When x=0, then t=1 and when x=π2, then t=2
∴I=2π∫21dtt2=2π[tan−2+1−2+1]21=−2π[1t]21
=−2π[12−1]
=−2π(−12)=π
According to the explanation , I=π
|
Updated on:21/07/2023
Related Playlists
- BOOK - NDA PREVIOUS YEARSCHAPTER - DEFINITE INTEGRATION & ITS APPLICATIONEXERCISE - DIRECTIONS60videos
DEFINITE INTEGRATION & ITS APPLICATION
- BOOK - NDA PREVIOUS YEARSCHAPTER - CONICS - PARABOLA, ELLIPSE & HYPERBOLAEXERCISE - MATH62videos
CONICS - PARABOLA, ELLIPSE & HYPERBOLA
- BOOK - NDA PREVIOUS YEARSCHAPTER - DERIVATIVESEXERCISE - MCQs94videos
DERIVATIVES
Similar Questions
∫π0sinxdx
View Solution∫π0logxdx
View SolutionConsider I=∫π0xdx1+sinx
What is ∫π0dx1+sinx equal to ?View Solution∫π0xdx1+sinx is equal to
View Solution∫π0tanxdx
View SolutionConsider I=∫π0xdx1+sinx
What is ∫π0(π−x)dx1+sinx equal to ?View SolutionConsider the integrals
A=∫π0sinxdxsinx+cosx and B=∫π0sinxdxsinx−cosx
What is the value of B ?View Solution∫π01+sinxdx
View SolutionThe value of the integral I=∫100π0dx1+esinx is equal to
View Solution∫π/20cosx1+sinxdx is equal to
View Solution