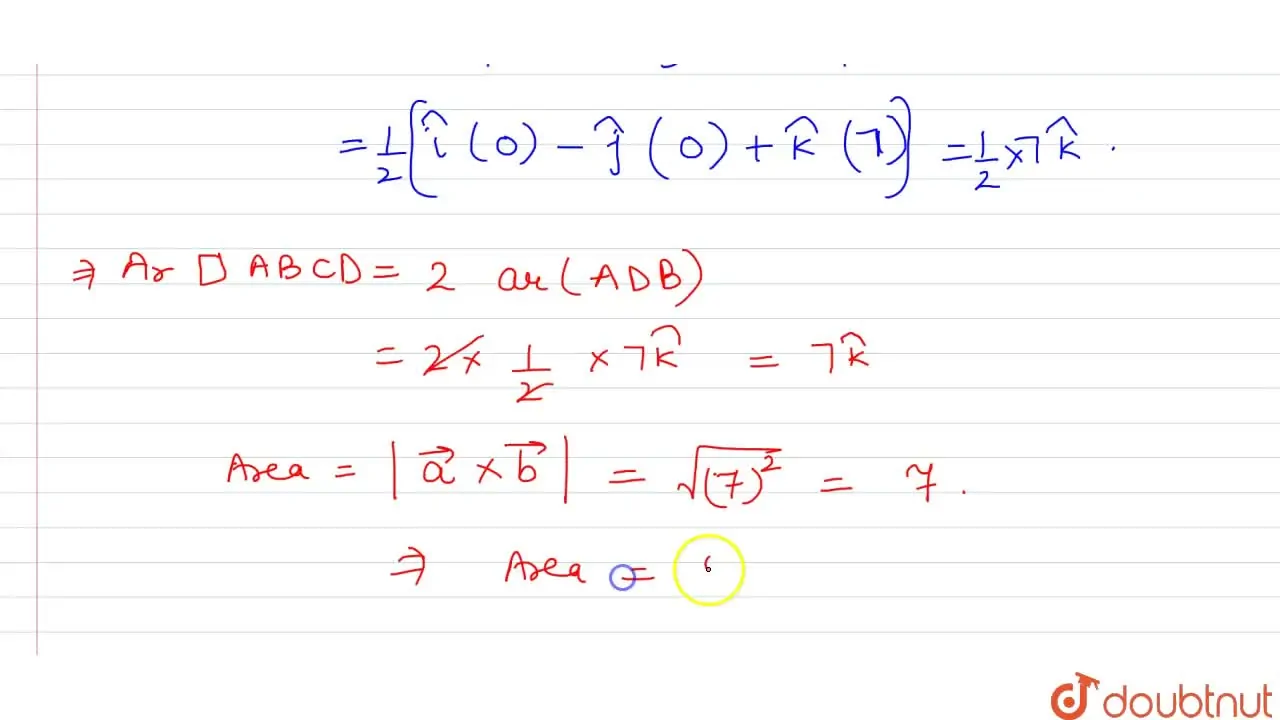Consider a parallelogram whose vertices are A (1, 2), B (4, y), C (x, 6) and D (3, 5) taken in order.
What is the area of the parallelogram ?
72 square units
4 square units
112 square units
7 square units
The correct Answer is:D
Area of parallelogram =2 area of ΔADB
→a=−−→AB=(4−1)ˆi+(3−2)ˆj
→b=−−→AB=(3−1)ˆi+(5−2)ˆj
∴ Area of parallelogram =2[12∣∣→a×→b∣∣]=∣∣→a×→b∣∣
Now, →a×→b=∣∣
∣
∣∣ˆiˆjˆk310230∣∣
∣
∣∣=7ˆk
∴ Area =∣∣→a×→b∣∣=∣∣7ˆk∣∣=√49=7 square unit
Related Playlists
Similar Questions
Consider a parallelogram whose vertices are A (1, 2), B (4, y), C (x, 6) and D (3, 5) taken in order.
What is the value of AC2−BD2 ?View SolutionConsider a parallelogram whose vertices are A (1, 2), B (4, y), C (x, 6) and D (3, 5) taken in order.
What is the point of intersection of the diagonals ?View SolutionThe vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6), D(3, 5), then (x, y) =
View SolutionThe vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6), D(3, 5), then (x, y) =
View SolutionThe vertices of a parallelogram in order are A(1,2), B(4, y), C(x, 6) and D(3,5). Then (x, y) is
View SolutionThe vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6), D(3, 5), then (x, y) =
View SolutionThe vertices of a parallelogram in order are A(1,2),B(4,y),C(x,6) and D(3,5) . Then (x,y) is :
View SolutionFind the area of a rectangle whose vertices are A(-2, 6), B (5,3), C (-1,-11) and D(-8,-8)
View SolutionFind the area of the quadrilateral whose vertices are A(1,1),B(3,4),C(5,−2) and D(4,−7)
View SolutionThree vertices of a parallelogram are (1, 1), (2, 4) and (3,5), then the fourth vertex of the parallelogram can be:
View Solution