Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of a is Solution in Tamil
1
3
2
-2
The correct Answer is:3
As the lines are perpendicular, Coefficient of x2+ Coefficient of y2=0
∴a−2=0
or a=2
Also , abc+2fgh−af2−bg2−ch2=0
∴c=−3
Hence , the given pair of lines is
2x2+3xy−2y2−5x+5y−3=0
Factorizing , we get lines
x+2y−3=0and2x−y+1=0
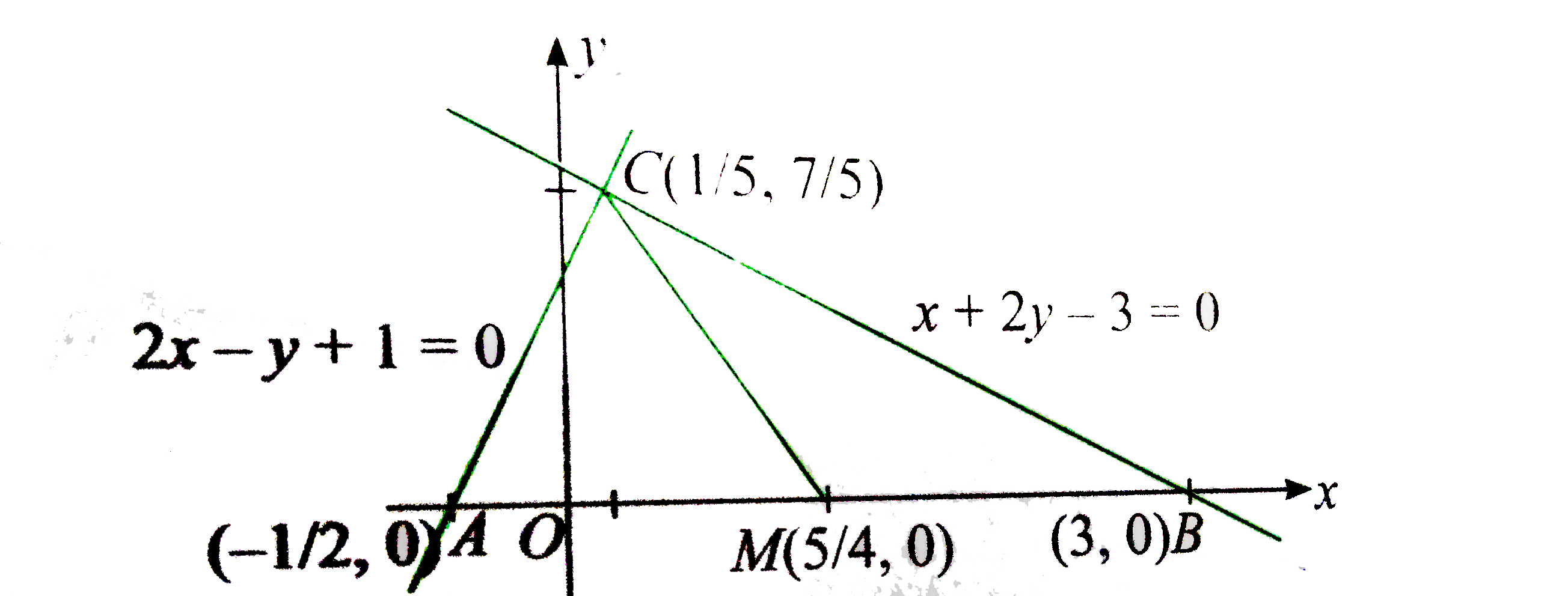
The point of intersection of the lines is C (1/5,7/5).
The points of intersection of the lines with the x- axis are A(3,0) and B (−1/2,0).
The orthocenter of triangle is C (1/5,7/5) and the circumcenter is the midpoint of AB which is M (5/4,0). Therefore,
CM√(54−15)2+4925=74
Related Playlists
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Multiple)9videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank9videos
PARABOLA
Similar Questions
The distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
01:11View SolutionThe equation x3+x2y−xy2=y3 represents
01:49View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?View SolutionThe equation of the latus rectum of a parabola is x+y=8 and the equation of the tangent at the vertex is x+y=12. Then find the length of the latus rectum.
02:16View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of a is04:03View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of c is02:53View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC is03:43View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x=5y+2=0
The value of λ is07:16View SolutionConsider a pair of perpendicular straight lines 2x2+3xy+by2−11x+13y+c=0 The value fo c is
06:27View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of a is08:43View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of c is04:40View SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC is08:54View SolutionThe point of intersection of the perpendiecular lines ax2+3xy−2y2−5x+5y+c=0 is
01:59View SolutionStatement I . The equation 2x2−3xy−2y2+5x−5y+3=0 represents a pair of perpendicular straight lines.
Statement II A pair of lines given by ax2+2hxy+by2+2gx+2fy+c=0 are perpendicular if a+b=004:46View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x=5y+2=0
The value of λ is00:53View Solution


