Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC is
4
9/2
8/3
7/4
The correct Answer is:4
As the lines are perpendicular, Coefficient of x2+ Coefficient of y2=0
∴a−2=0
or a=2
Also , abc+2fgh−af2−bg2−ch2=0
∴c=−3
Hence , the given pair of lines is
2x2+3xy−2y2−5x+5y−3=0
Factorizing , we get lines
x+2y−3=0and2x−y+1=0
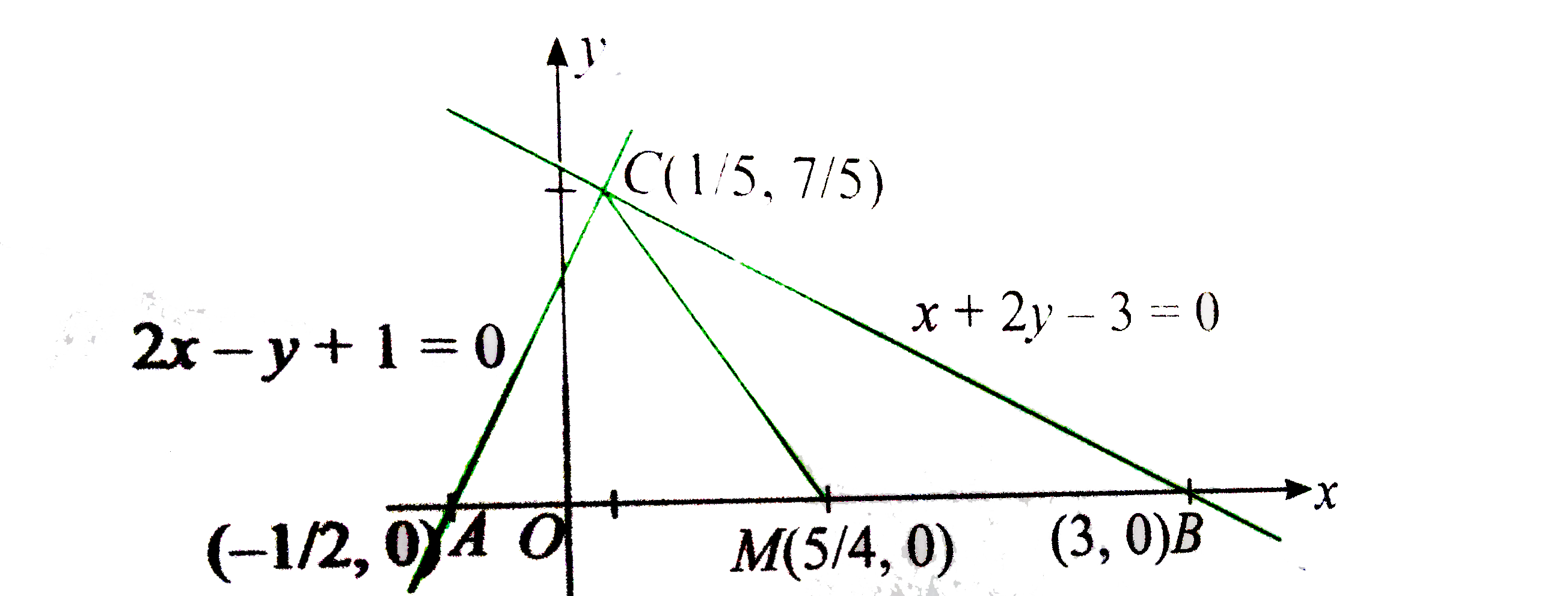
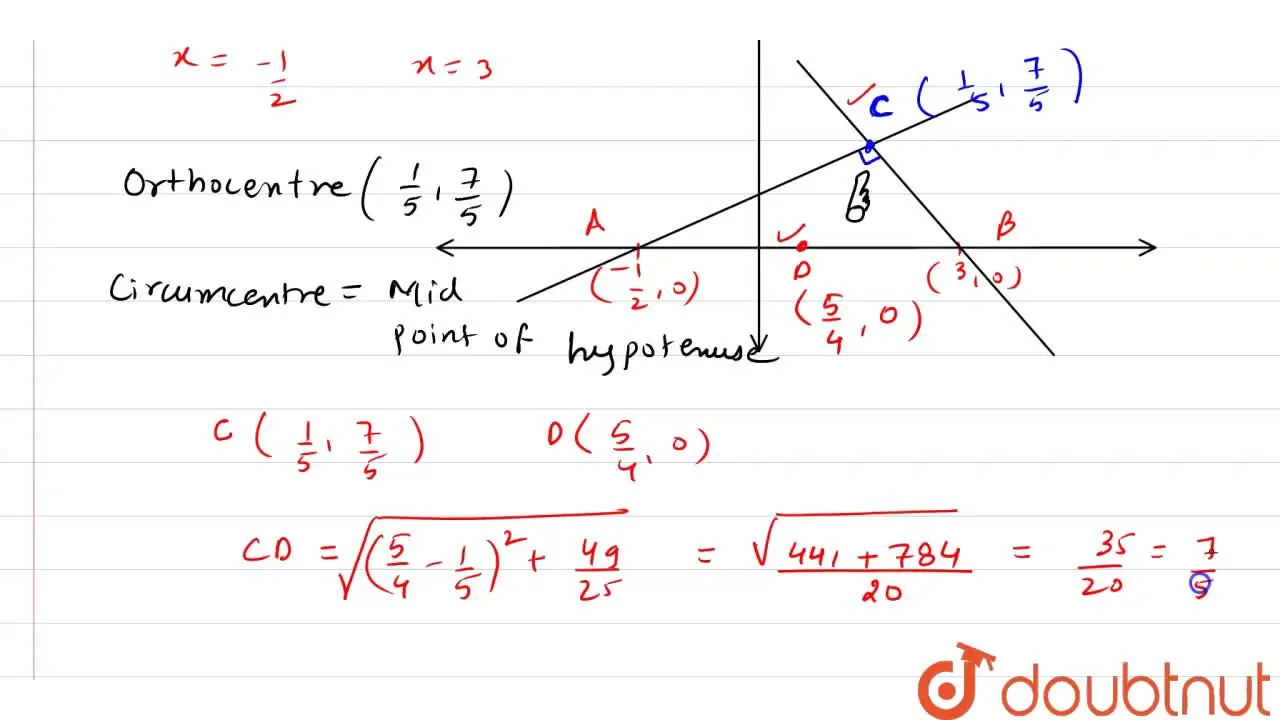
The point of intersection of the lines is C (1/5,7/5).
The points of intersection of the lines with the x- axis are A(3,0) and B (−1/2,0).
The orthocenter of triangle is C (1/5,7/5) and the circumcenter is the midpoint of AB which is M (5/4,0). Therefore,
CM√(54−15)2+4925=74
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Multiple Correct Answer Type9videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Matching Column Type1videos
PARABOLA
Similar Questions
Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of c isView SolutionConsider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
The value of a isView SolutionConsider a pair of perpendicular straight lines 2x2+3xy+by2−11x+13y+c=0 The value fo c is
View SolutionConsider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR isView SolutionFind the angle between the pair of straight lines x2−3xy+2y2=0
View SolutionConsider the equation of a pair of straight lines as 2x2−10xy+12y2+5x−16y−3=0. The angles between the lines is θ . Then the value of tanθ is
View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x−5y+2=0
The angle between the lines is θ then the value of cos 2θ isView SolutionFindthe angle between the pair of straight lines x2−4y2+3xy=0
View SolutionThe equation to the pair of lines perpendicular to the pair of lines 3x2−4xy+y2=0, is
View SolutionConsider the equation of a pair of straight lines as x2−3xy+λy2+3x=5y+2=0
The value of λ isView Solution