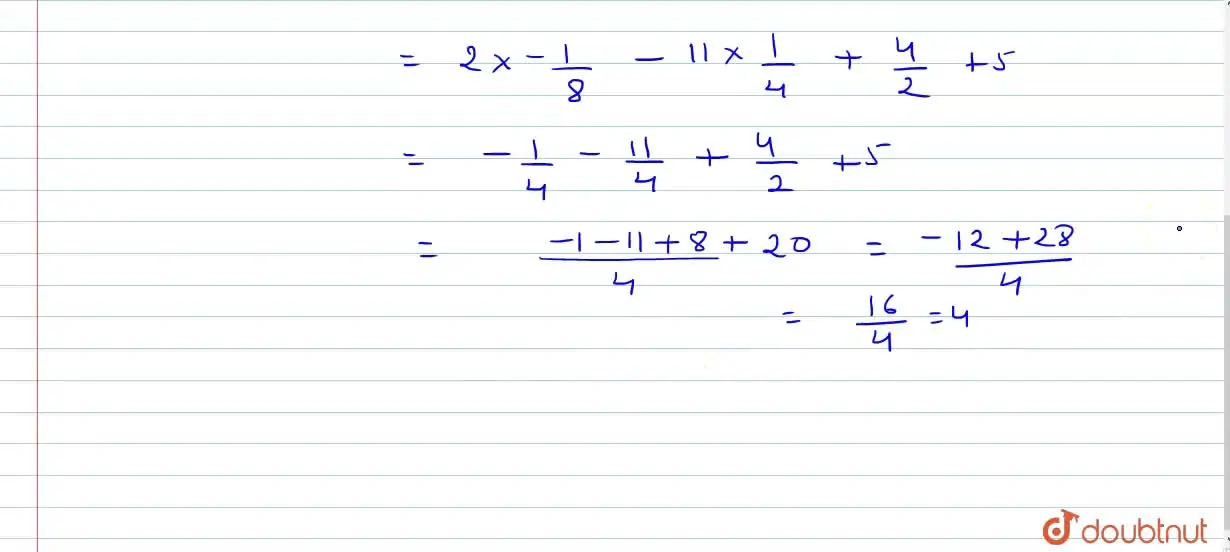check whether p(x) is a multiple of g(x) or not
(i) p(x)=x3−5x2+4x−3,g(x)=x−2.
(ii) p(x)=2x3−11x2−4x+5,g(x)=2x+1
(i) ∵g(x)=x−2 [given ]
then zero of g(x) is 2.
Now p(2)=(2)3−5(2)2+4(2)−3[∵p(x)=x3−5x2+4x−3,given ]
=8−20+8−3=−7≠0
Since , remainder ≠ 0, So p(x) is not a multiple o fg(x).
(ii) here ,g(x) =2x+1.
then ,zero of g(x) is −12
Now ,(−12)=2(−12)3−11(−12)2−4(−12)+5[∵p(x)=2x3−11/x2−4x+5]
=2(−18)−11(14)+2+5=−14−114+7
=−1−1+284=164=4
SInce , remainder ≠ SO p(x) is not a multiple of g(x) .
Related Playlists
Similar Questions
f(x)=4x3−12x2+14x−3, g(x)=2x−1
View SolutionCheck whether q(x) is a multiple of r(x) or not.
Where q(x)=2x3−11x2−4x+5,r(x)=2x+1View SolutionBY Remainder theorem , find the remainder when p(x) is divided by g(x)
(i) p(x) =x3−2x2−4x−1,g(x)=x+1
(ii) p(x)=x3−3x2+4x+50,g(x)=x−3View SolutionUse the factor theorem, to determine whether g(x) is a factor of p(x) in each of the following cases :
(i) p(x)=2x3+x2−2x−1,g(x)=x+1
(ii) p(x)=x3+3x2+3x+1,g(x)=x+2
(iii) p(x)=x3−4x2+x+6,g(x)=x−3View Solutioncheck whether g(x) is a factor of f(x) or not f(x)=x5+3x4−x3−3x2+5x+15, g(x)=x+3
View SolutionUse the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:(i) p(x)=2x3+x2−2x−1,g(x)=x+1
(ii) p(x)=x3+3x2+3x+1,g(x)=x+2
(iii) p(x)=x3+4x2+x+6,g(x)=x−3View SolutionCheck whether g(x) is a factor of p(x) by dividing the first polynomial by the second polynomial:
(i) p(x)=4x3+8x+8x2+7,g(x)=2x2−x+1, (ii) p(x)=x4−5x−2,g(x)=2−x2, (iii) p(x)=13x3−19x2+12x+14,g(x)=2−2x+x2View SolutionDivide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x)= x3−3x2+5x−3,g(x)=x2−2 (ii)p(x)=x4−3x2+4x−5,g(x)=x2+1−x (iii)p(x)=x4−5x+6,g(x)=2−x2View Solution(iv) Divide P(x)=2x2−3x+5 by g(x)=x−3
View SolutionIf p(x)=x3−5x2+4x−3andg(x)=x−2 show that p(x) is not a multiple of g(x).
View Solution