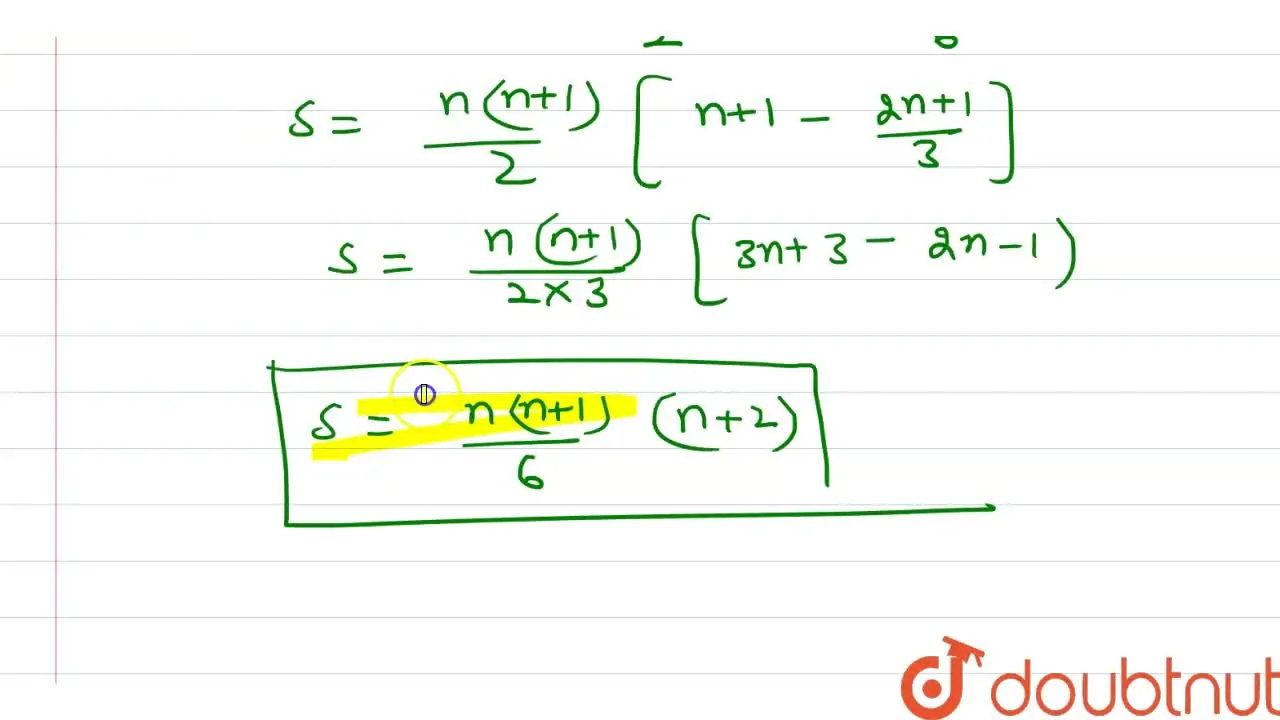
श्रेणी का योगफल ज्ञात कीजिए।
माना श्रेणी का r वां पद है।
Related Playlists
Similar Questions
किसी अनुक्रम का n वां पद Tn निम्न प्रकार परिभाषित है। इसके प्रथम चार पद ज्ञात कीजिए :
(a) Tn=3n+1
(b) Tn=n2+5
(c ) Tn=n(n+1)
(d) Tn=n+1n
(e ) Tn=3n.04:46View Solutionएक श्रेणी का n वां पद (3n+5) है सिद्ध कीजिए कि यह श्रेणी समांतर श्रेणी है। इसका 6 वां पद भी ज्ञात कीजिए।
04:51View Solution'DAUGHTER ' शब्द के अक्षरों से , कितने अर्थपूर्ण या अर्थहीन शब्दों की रचना की जा सकती है , जबकि प्रत्येक शब्द में 2 स्वर तथा 3 व्यंजन हों ?
05:28View SolutionFind the sum of the series: 1.n+2.(n−1)+3.(n−2)++(n−1).2+n.1.
05:17View SolutionThe sum of the series 11!(n−1)!+13!(n−3)!+15!(n−5)!+…..+1(n−1)!1! is = (A) 1n!2n (B) 2nn! (C) 2n−1n! (D) 1n!2n−1
04:22View SolutionProve that 1⋅2+2⋅3+3⋅4+.....+n⋅(n+1)=n(n+1)(n+2)3
06:02View SolutionIf 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!=(n+1)!−1 then show that, 1⋅1!+2⋅2!+3⋅3!+...+n⋅n!+(n+1)(n+1)!=(n+2)!−1
06:06View Solutionनिम्न श्रेढियों के n पदों तक का योगफल ज्ञात कीजिए -
1+2+5+12+25+46+……..04:49View Solutionनिम्न श्रेढियों के n पदों तक का योगफल ज्ञात कीजिए -
1+4+13+40+121+……..02:24View Solutionश्रेणी 1+45+752+1053+….. के n पदों का योगफल है -
07:25View SolutionA) |lim_(n rarr oo)((n^((1)/(2)))/(n^((3)/(2)))+(n^((1)/(2)))/((n+3)^((3)/(2)))+....+(n^((1)/(2)))/( n+3(n-1) ^((3)/(2))))=
03:12View SolutionLet Sn=1+12+13+….+1n Show that nsn=n+(n−11+n−22+………+2n−2+1n−1).
05:45View Solutionनिम्नलिखित श्रेणी का योग ज्ञात कीजिए :
1+45+752+1053+...........n पदों तक ।05:25View SolutionFind the sum of the series: 1.n+2.(n−1)+3.(n−2)++(n−1).2+n.1.
03:05View SolutionThe value of limn→∞1.n+2.(n−1)+3.(n−2)+...+n.112+22+...+n2
06:39View Solution