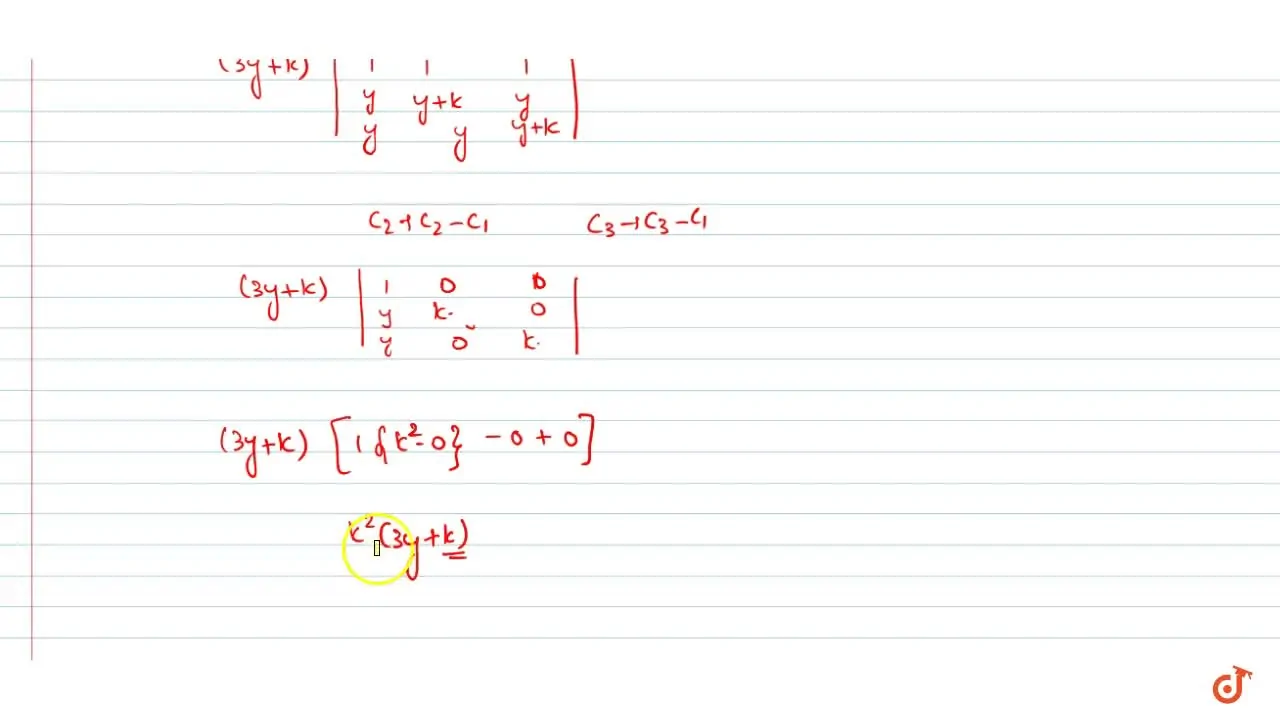By using properties of determinants. Show that:
(i)
(ii)
(i)
Applying
Applying and
(ii)
Applying
Applying and
Related Playlists
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.518videos
DETERMINANTS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.18videos
DETERMINANTS
- BOOK - NCERTCHAPTER - DETERMINANTSEXERCISE - EXERCISE 4.45videos
DETERMINANTS
- BOOK - NCERTCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - QUESTION3videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
Similar Questions
Using properties of determinants , find the value of k if
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=k(x3+y3).View SolutionUsing properties of determinants, prove the following ∣∣ ∣ ∣∣xx+yx+2yx+2yxx+yx+yx+2yx∣∣ ∣ ∣∣=9y2(x+y)
View SolutionShow that: (x2+y2)5=(x5−10x3y2+5xy4)2+(5x4−10x2y3+y5)2
View SolutionIf∣∣ ∣ ∣∣x+y+2zxyzy+z+2xyzxz+x+2y∣∣ ∣ ∣∣=k(x+y+z)3, then the value of k is
View SolutionDetermine the value of x+yx+2y when 2x+yx+4y = 3
View Solution2x−3y=k4x+5y=3
View SolutionIf x2dydx=y(x+y)2, then (y−x)2=kx2y
View SolutionThe distance between the directrices of the ellipse (4x−8)2+16y2=(x+√3y+10)2 is k, then k2 is
View SolutionFor which of the following, y can be a function of x, (x∈R,y∈R)?
(i)(x−h)2+(y−k)2=r2(ii)y2=4ax(iii)x4=y2(iv)x6=y3(v)3y=(logx)2View SolutionSimplify:
(2x+5y)(3x+4y)−(7x+3y)(2x+y)View Solution