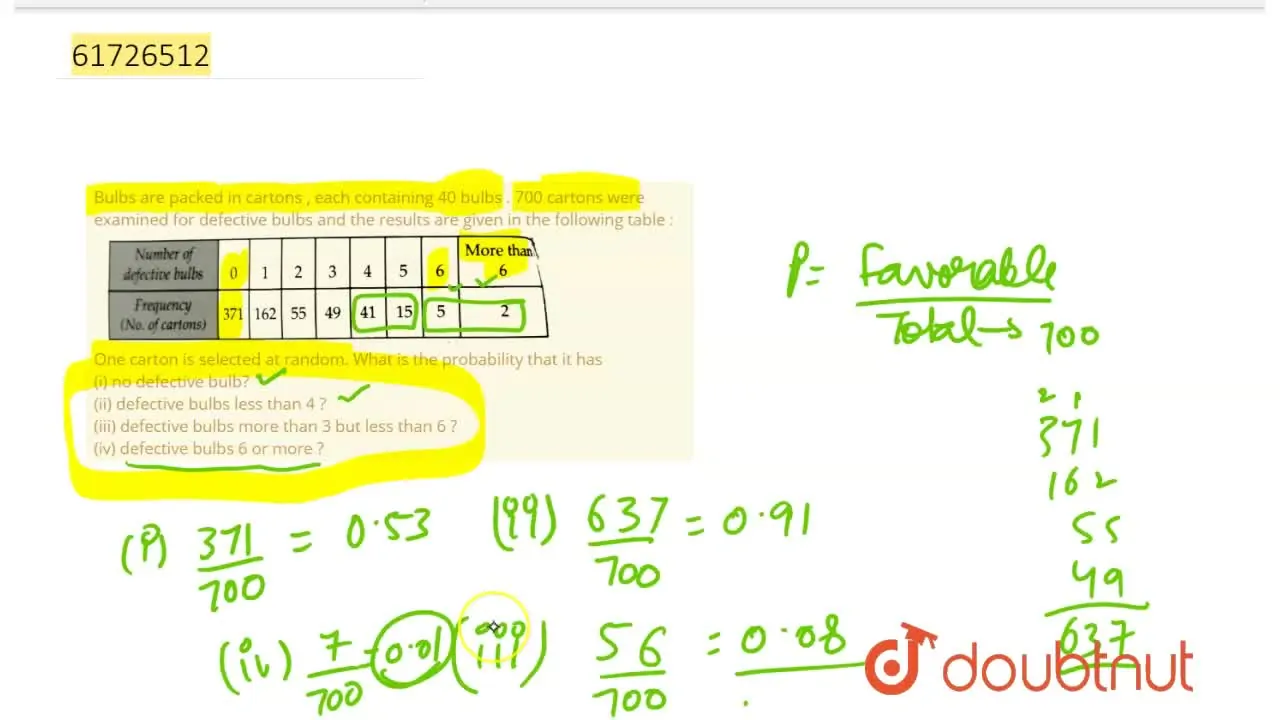
Bulbs are packed in cartons , each containing 40 bulbs . 700 cartons were examined for defective bulbs and the results are given in the following table :

One carton is selected at random. What is the probability that it has
(i) no defective bulb?
(ii) defective bulbs less than 4 ?
(iii) defective bulbs more than 3 but less than 6 ?
(iv) defective bulbs 6 or more ?
Total number of cartons = 700 .
(i) Let E1 be the event of choosing a carton having no defective bulb . Then ,
P (choosing a carton having no defective bulb)
=P(E1)
= number of cartons having 0 defective bulbtotal number of cartons
=371700=53100=0.53.
(ii) Let E2 be the event of choosing a carton having defective bulbs less than 4 . then,
P (choosing a carton having defective bulbs less than 4)
=P(E2)
= number of cartons having defective bulbs 0 , 1 , 2 or 3total number of cartons
371+162+55+49700=637700=91100=0.91.
Let E3 be the event of choosing a carton having defective bulbs more than 3 but less than 6 . Then ,
P (choosing a carton having defective bulbs more than 3 , but less than 6)
=P(E3)
number of cartons having defective bulbs 4 or 5total number of cartons
= 41+15700=56700=8100=0.08 .
(iv) Let E4 be the event of choosing a carton having defective bulbs 6 or more . then ,
P(choosing a carton having defective bulbs 6 or more )
P(E4)
= number of cartons having defective bulbs 6 or moretotal number of cartons
=5+2700=7700=1100=0.01.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 1918videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PRESENTATION OF DATA IN TABULAR FORMEXERCISE - Multiple Choice Questions (Mcq)9videos
PRESENTATION OF DATA IN TABULAR FORM
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
Similar Questions
Bulbs are packed in carbons each containing 40 bulbs, seven hundred cartons were examined for defective bulbs and the results are given in the following table.

One carton was selected at random. What is the probability that it has
i) no defective bulb?
ii) defective bulbs from 2-6?
iii) defective bulbs less than 4?View SolutionBulbs are packed in cartons each containing 40 bulbs. Seven hundred cartons were examined for defective bulbs and the results are given in the following table :
Number of defective bulbs 0 1 2 3 4 5 6 More than 6Frequency400 180 48 41 18 8 3 2
One carton was selected at random. What is the probaility that it has
(i) no defective bulbs ?
(ii) defective buble from 2 to 6 ?
(iii) defective bulbs less than 4 ?View SolutionOver the past 200 working days , the number of defective parts produced by a machine is given in the following table :
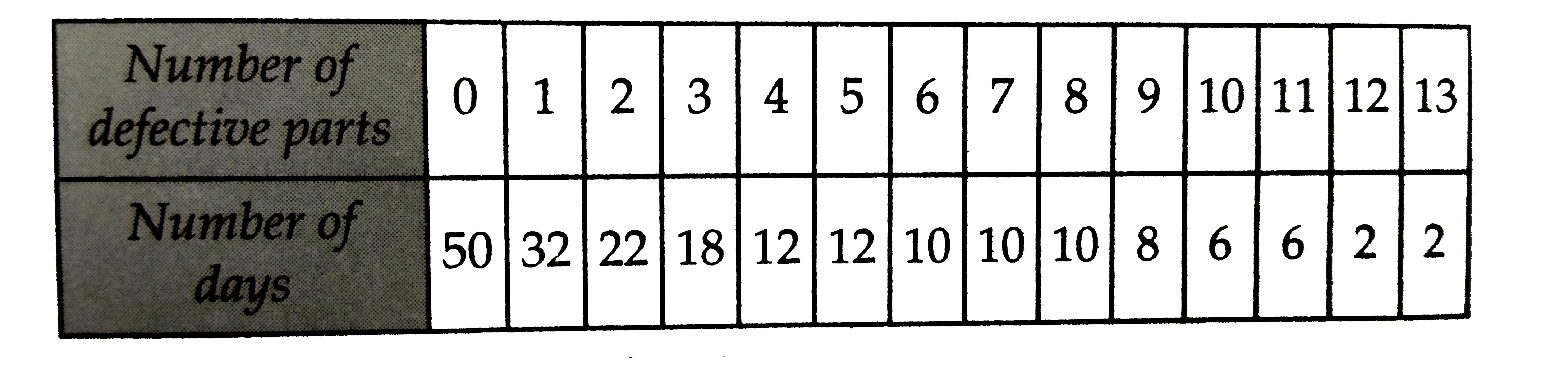
From these days , one day is chosen at random . What is the probability that on that day , the output has
(i) no defective part ?
(ii) at least 1 defective part ?
(iii) not more than 5 defective parts ?
(iv) more than 5 , but less than 8 defective parts ?
(v) more than 13 defective parts ?View SolutionA lot of 20 bulbs contains 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
View SolutionA lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
View SolutionIt is known that a box of 100 electric bulbs contains 8 defective bulbs. One bulb is taken out at random from the box. What is the probability that the bulb drawn is (i) defective? (ii) non -defective?
View SolutionIt is known that a box of 200 electric bulbs contains 16 defective bulbs. One bulb is taken out at random from the box. What is the probability that the bulb drawn is (i) defective, (ii) non-defective?
View SolutionSuppose the bulb drawn in (i) is not defective and not replaced. Now bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
View SolutionIn a box containing 60 bulbs 6 are defective . What is the probability that out of a sample of 5 bulbs (i) none is defective (ii) exactly 2 are defective ?
View SolutionIn a box containing 100 bulbs, 10 are defective. What is the probability that out of a sample of 5 bulbs, (i) none is defective and (ii) exactly 2 are defective ?
View Solution