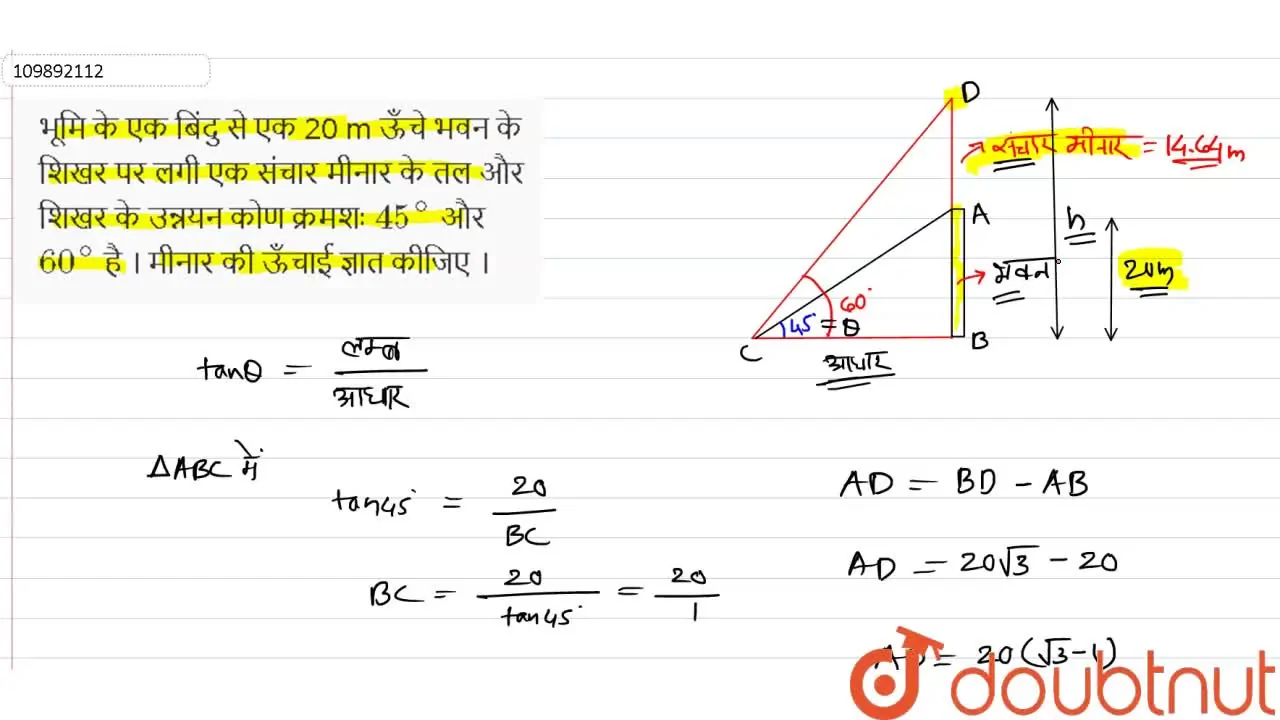
भूमि के एक बिंदु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45∘ और 60∘ है । मीनार की ऊँचाई ज्ञात कीजिए ।
मान ले कि CD भवन है और AD संचार मीनार है ।
मान ले मीनार कि ऊँचाई = AD
दिया है , भवन कि ऊँचाई CD = 20 m
बिंदु B पर मीनार के तल का उन्नयन कोण =45∘
मीनार के शिखर का उन्नयन कोण=60∘
समकोण ΔBCD में ,
tan45∘=CDBC⇒1=20BC⇒BC=20 m ... (i)
पुनः समकोण ΔABC में , tan60∘=ACBC⇒√3=AC20
⇒AC=20√3 m ...(ii)
अब AC=AD+CD ⇒AD=AC−CD
⇒AD=20√3−20=20(√3−1)m ,
अतः मीनार कि ऊँचाई AD=20(√3−1) m

Related Playlists
- BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - अतिलघु उत्तरीय प्रश्न4videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - लघु उत्तरीय प्रश्न33videos
त्रिकोणमिति के कुछ अनुप्रयोग
- BOOK - KC SINHACHAPTER - 2018 BEXERCISE - प्रश्न32videos
2018 B
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
Similar Questions
△ABC में ∠A=90∘ , AB=12cm और AC=4√3cm, तब ∠B ज्ञात करे।
04:23View Solution△ABC एक समकोण त्रिभुज है जिसमे AB=8 m , ∠BCA=30∘ तब ज्ञात करे :
(i) C से A का उन्नयन कोण ।
(ii) A से C का अवनयन कोण ।
(iii) BC और AB06:40View Solutionयूक्लिड विभाजन एल्गोरिदम की मदद 870 तथा 225 का महत्तम समावर्तक निकालें ।
00:59View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..05:44View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
02:27View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
03:00View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
02:14View Solution60 मी ऊँचे एक भवन से एक प्रकाश स्तंभ की चोटी और आधार के उन्नयन और अवनमन कोण क्रमश : 30∘ और 60∘ हैं । ज्ञात कीजिए :
( i ) प्रकाश स्तंभ और भवन की ऊँचाइयों में अंतर ।
( ii ) प्रकाश स्तंभ और भवन के बीच की दूरी ।03:32View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
05:15View Solutionएक रेखा की दिक्-कोसाइन ज्ञात कीजिए तो निर्देशांक्षो के साथ समान कोण बनाती है |
49:45View SolutionA tower stands on the top of a building which is 40 metres high. The angle of depressiotf of a point situated on the ground-from the top and bottom of the tower are found to Be 60∘ and 45∘ respectively.What is the height (in metres) of tower?
एक भवन जिसकी ऊँचाई 40 मीटर है, के शिखर पर एक मीनार खड़ी है। मीनार के शिखर तथा पांद बिन्दु से भूमि पर स्थित एक बिन्दु का अर्वनमन कोण क्रमशः 60∘ तथा 45∘ है। मीनार की ऊँचाई (मीटर में) क्या है ?04:30View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
02:27View SolutionA vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angle of elevation of the bottom of the flag staff is alpha and that of the top of the flag staff is beta . then the height of the tower is एक ऊर्ध्वाधर मीनार एक क्षेतिज समतल पर खड़ी है और उसके ऊपर 1 ऊँचाई का ऊर्ध्वाधर ध्वजखण्ड लगा है। समतल पर एक बिन्दु पर ध्वजदण्ड के तल का उन्नयन कोण alpha है और ध्वजदण्ड के शीर्ष भाग का beta है। मीनार की ऊँचाई बताइए ?
01:39View Solutionएक कोण पर झुके हुए तल पर ऊँचाई से प्रक्षेप्य
02:33View SolutionFrom the top of a 10 m high building, the angle of elevation of the top of a tower is 60^@ and the angle of depression of the foot of the tower is Theta , such that tan Theta = 2/3 . What is the height of the tower to nearest metres? 10 मी ऊँची इमारत से किसी मीनार के शीर्ष का उन्नयन कोण 60^@ है तथा मीनार के तल का अवनमन कोण Theta इस प्रकार है कि tan Theta = 2/3 है | निकटतम मीटर तक मीनार की ऊंचाई ज्ञात करें |
05:27View SolutionThe angle of elevation of top of a tower from a point P, on the ground is theta such that tan theta =12/5 . If distance of the point P,from the base of the tower is 75m, what is the height of the tower? भूमि पर स्थित एक बिंदु P से किसी मीनार के शीर्ष का उन्नयन कोण theta इस प्रकार है कि tan theta =12/5 है| यदि मीनार के तल से बिंदु P की दूरी 75 मीटर है, तो मीनार की ऊंचाई क्या है ?
03:43View Solution