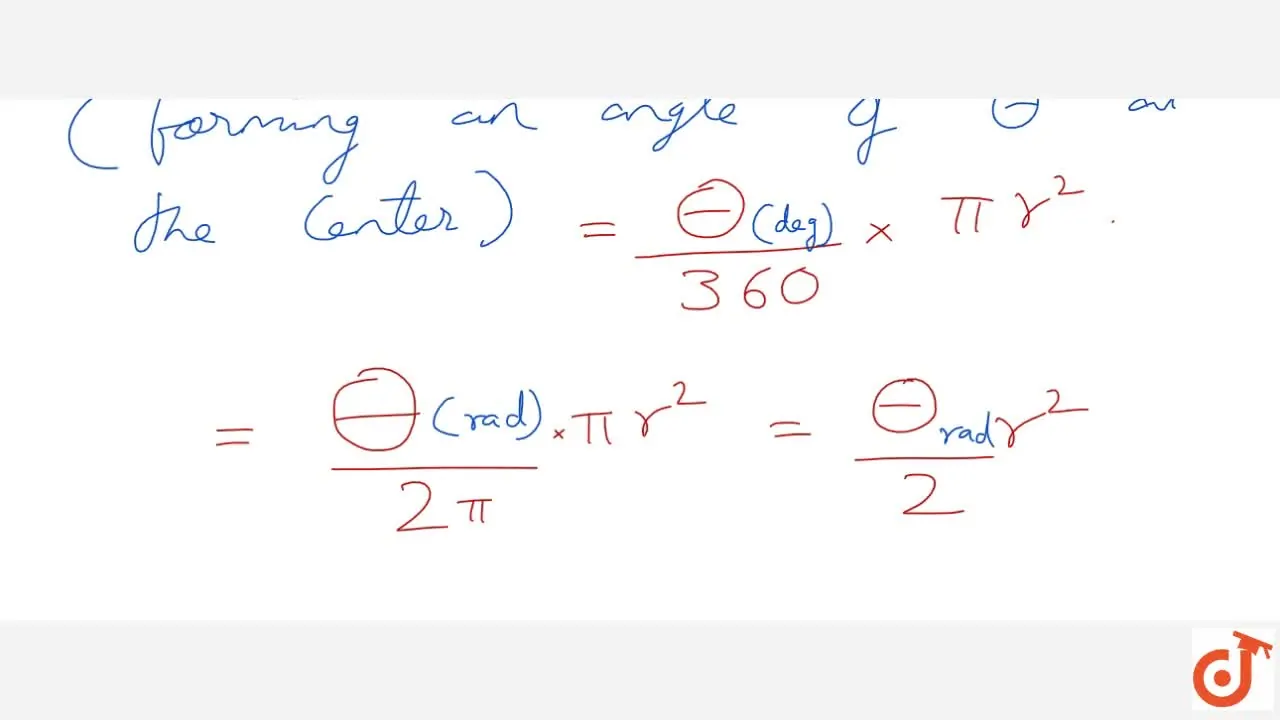Area of a sector
Step by step video & image solution for Area of a sector by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Find the areas of a sector of angle 120∘ and is corresponding major sector of a circle of radius 21cm.
View SolutionIf ABCD is a square, then the area of the sector shown in the figure is
 View Solution
View SolutionArea of the sector is ………….time the length of its corresponding are
View SolutionThe length of the perimeter of a sector of a circle is 20 cm, the maximum area of the sector is
View SolutionThe perimeter of a sector is p. The area of the sector is maximum when its radius is
View SolutionThe angle of a sector is 120∘ and its radius is 21 cm.
The area of the sector is ______.View SolutionThe angle of a sector is 120∘ and its radius is 21 cm.
The area of the sector is ______.View SolutionThe angle of a sector of radius 14 cm is 90∘. The area of the sector is ________.
View SolutionThe angle of a sector of radius 14 cm is 90∘. The area of the sector is ________.
View SolutionThe angle of a sector of a circle is 90∘. The ratio of the area of the sector and that of the circle is ______.
View Solution