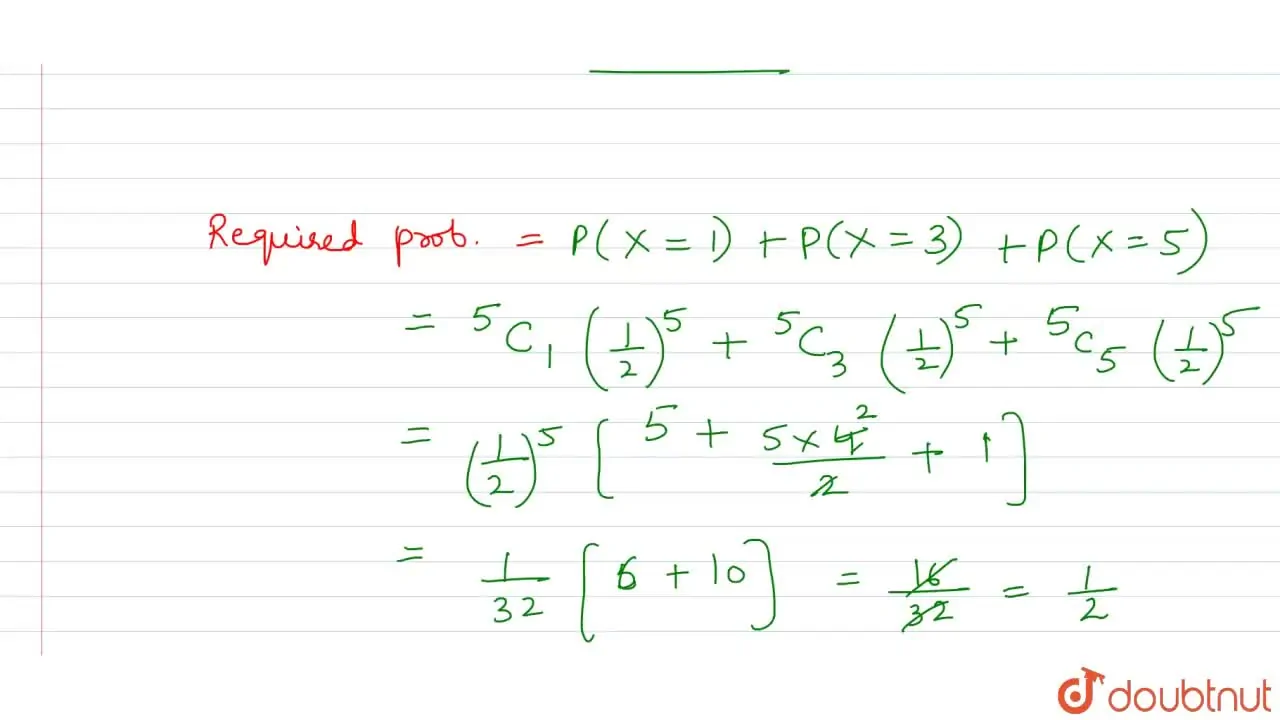An ordinary dice is rolled a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even numebr 3 times. Then the probability of getting an odd number and odd number of times, is
1/32
5/16
1/2
none of these
The correct Answer is:C
Let the dice be rolled n times.
We have,
p=probabiilty of getting odd number in a throw =12
∴ Probability of getting an odd number 2 times
=.Nc2(12)2(12)n−2=.nC2(12)n
Similarly, we have
Probability of getting an even number 3 times
=.Nc3(12)2(12)n−3=.nC3(12)n
It is given that
=.Nc2(12)n=.nCr(12)n⇒.nC3=.nC3⇒n=5
Let X denote the number of times an odd number is obtained in n throws of the dice. Then,
P(X=r)=.nCr(12)r(12)n−r=.nCr(12)2=.5Cr(12)5
∴ Required probability
=P(X=1)+P(X=3)+P(X=5)
=.5C1(12)5+.5C3(12)5+.5C5(12)5=12.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Section II - Assertion Reason Type1videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise40videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise40videos
DISCRETE PROBABILITY DISTRIBUTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DETERMINANTSEXERCISE - Chapter Test30videos
DETERMINANTS
- BOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test30videos
FUNCTIONS
Similar Questions
An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is :
View SolutionA die is rolled n times. If the probability of getting odd number 2 times is equal to the probability of getting even number 3 times. Find the probability of getting odd number odd times
View SolutionA fair die is thrown n times. The probability of getting an odd number twice is equal to that getting an even number thrice. The probability of getting an odd number, odd number of times is
View Solution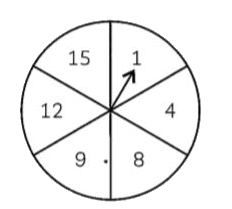
What is the probability of getting an odd number on the spinner?View SolutionA die is thrown once. find the probability of getting an odd number
View SolutionA die is thrown once. Find the probability of getting an odd number.
View SolutionIf an unbiased dice is rolled, then the probability of getting an even number is _______ then/to that of getting an odd number.
View SolutionA fair coin is tossed 100 times. What is the probability of getting tails an odd number of times?
View SolutionA fair coin is tossed 100 times the probability of getting tails an odd number of time is
View SolutionWhen a die is thrown, the probability of getting an odd number less than 3 is
View Solution