AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
7
14
17
20
The correct Answer is:B
Step by step video, text & image solution for AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A rectangle is 5 times as wide as it is long. The area of the rectangle is 320 square feet. What is the perimeter of the rectangle , in feet ?
View SolutionThe equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
View SolutionThe area of a rectangle is 10 sq. cm. Express the area in terms of sq. m
View SolutionThe area of a rectangle will be maximum for the given perimeter, when rectangle is a
View SolutionArea of a rectangle of breadth 17cm is 340cm2. Find the perimeter of the rectangle.
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
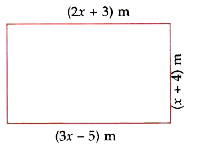 View Solution
View SolutionIn the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
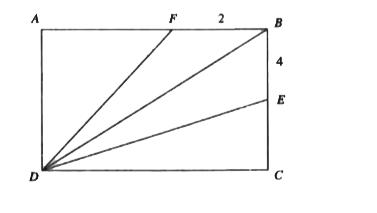 View Solution
View SolutionThe length of a rectangle exceeds its width by 8 cm and the area of the rectangle is 240 sq. cm. Find the dimensions of the rectangle.
View Solution
If the rectangle above has an area of 32, and the unshaded triangles are isosceles, what is the perimeter of the shaded area?View SolutionIn the figure, the ratio of the area of parallelogram ABCD to the area of rectangle AECF is 5 : 3. What is the area of the rectangle AECF?
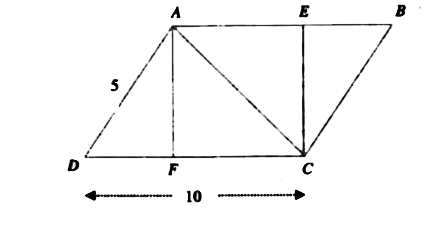 View Solution
View Solution


