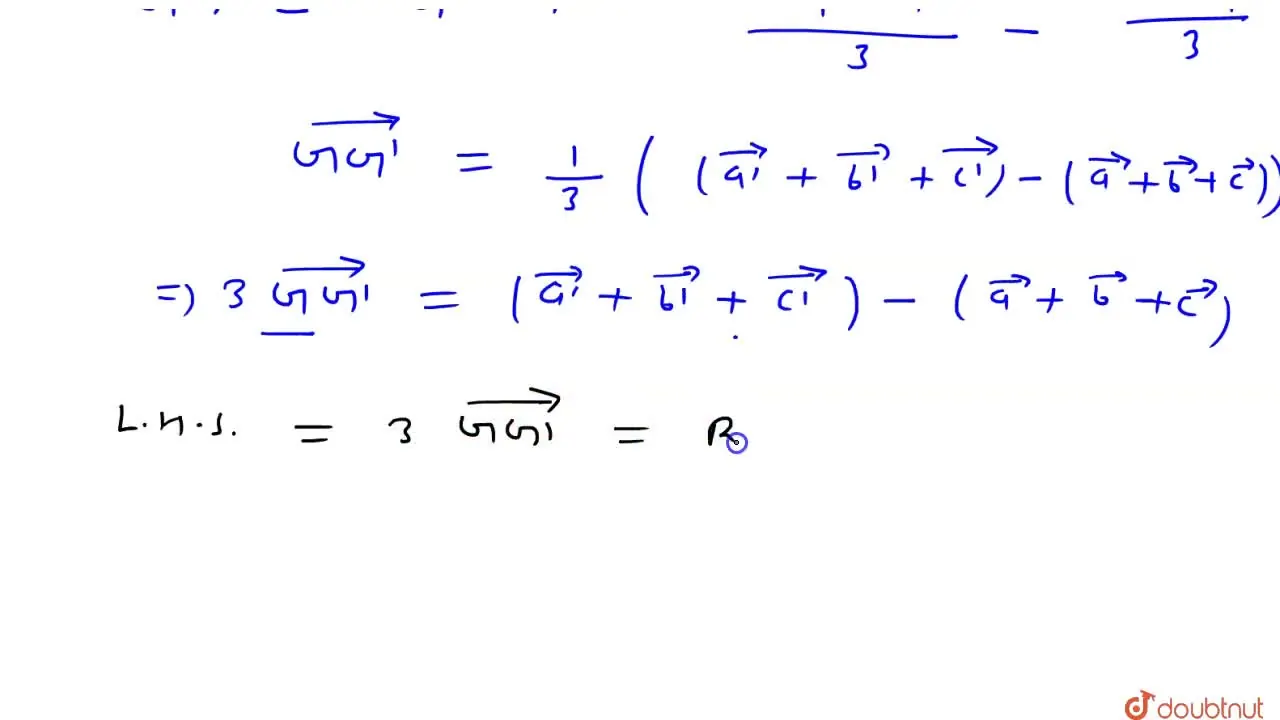ABC और A'B'C दो त्रिभुज है और G ,G ' उनके केन्द्रक है,तो दर्शाइए की-
→AA'+→BB'+→CC'=3→GG'
माना मूलबिंदु O के सापेक्ष A ,B ,C और A,'B',C' के स्थिति सदिश क्रमशः →a,→b,→c और →a',→b',→c' है,तब →AA'+→BB'+→CC'=(→a'−→a)+(→b'−→b)+(→c'−→c)=(→a'+→b+→c)−(→a+→b+→c) ....(i)
केन्द्रक G का स्थिति सदिश =→a+→b+→c3
केन्द्रक G ' का स्थिति सदिश =→a'+→b'+→c3
∴ →GG'=→a'+→b'+→c'3−→a+→b+→c3
⇒ →GG'=13[(→a'+→b'+→c')−(→a+→b+→c)]
⇒ 3→GG'=[(→a'+→b'+→c')−(→a+→b+→c)]
⇒ 3→GG'=→AA'+→BB'+→CC [समी(1 ) से]
⇒ →AA'+→BB'+→CC'=3→GG' यही सिद्ध करना था|
Related Playlists
- BOOK - PRABODH PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 22.127videos
सदिश बीजगणित
- BOOK - PRABODH PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - प्रश्नावली 22.24videos
सदिश बीजगणित
- BOOK - PRABODH PUBLICATIONCHAPTER - संबंध और फलन EXERCISE - दीर्घ उत्तरीय प्रश्न36videos
संबंध और फलन
- BOOK - PRABODH PUBLICATIONCHAPTER - समाकलनो के अनुप्रयोग EXERCISE - प्रश्नावली 20.48videos
समाकलनो के अनुप्रयोग
Similar Questions
सदिश के मापांक ज्ञात कीजिए| →a=ˆi+ˆj+ˆk
03:06View Solutionदर्शाइए की सदिश 2ˆi−3ˆj+4ˆk और −4ˆi+6ˆj−8ˆk संरेख है|
02:26View Solutionसिद्ध कीजिए कि समुच्चय {1,2,} में R={(1,1),(2,2),(3,3),(1,2),(2,3)} द्वारा प्रदत्त संबंध स्वतुल्य है परन्तु न तो सममित है और न संक्रामक है।
04:47View Solutionपरवलयो y2=4x और x2=4y से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
02:07View SolutionIf ABCandA'B'C are two triangles and G,G' be their centriods, prove that →∀'+→BB'+→C'=3→GG'
08:31View SolutionIf G is the centroid of triangle ABC,then→GA+→GB+→GC is equal to a. →0 b. 3→GA c. 3→GB d. 3→GC
03:28View SolutionIf G is the centroid of ΔABCandG' is the centroid of ΔA'B'C' then −−→AA'+−−→BB'+−−→CC'=
03:49View Solutionयदि →a=ˆi−ˆj+ˆk और →b=2ˆi+2ˆj−3ˆk तो ∣∣→a−2¯b∣∣ है |
02:17View Solutionयदि →A=→i+→j+→k,→C=→j−→k तो →B निकाले ताकि →A×→B=→C और →A.→B=3.
06:03View SolutionIf G is the centroid of Δ ABC then →GA+→GB+→GC=
01:47View SolutionIf G is the centroid of Δ ABC, G' is the centroid of Δ A' B' C' then →AA'+→BB'+→CC'=
04:06View Solutionयदि दो सदिशों →a और →b के बीच का कोण θ है तो →a.→b≥0 होगा। यदि -
01:48View SolutionIf the centroids of ΔABC and ΔA'B'C' are respectively G and G' then −−−→AA'+−−−→BB'+−−−→CC' ……………….. .
03:25View SolutionIf G is the centroid of triangle ABC,then→GA+→GB+→GC is equal to a. →0 b. 3→GA c. 3→GB d. 3→GC
02:52View SolutionIf G is the centroid of a triangle ABC, prove that →GA+→GB+→GC=→0.
03:54View Solution