Question

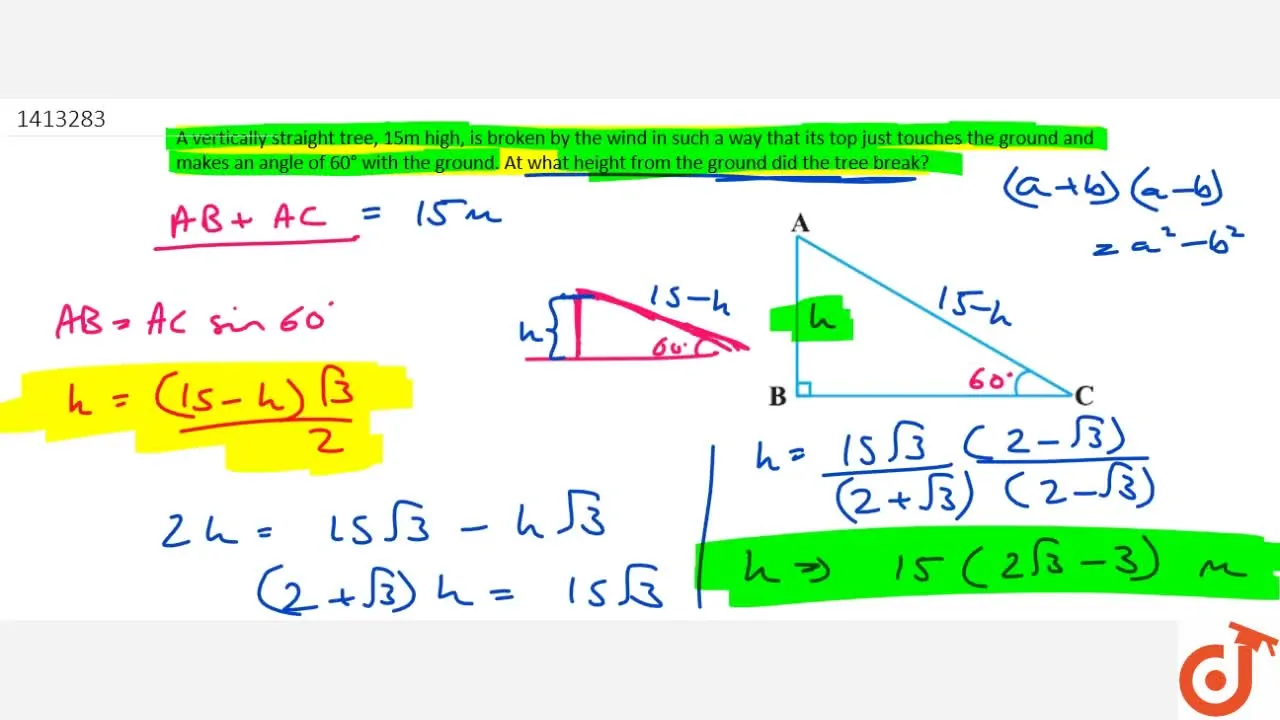
A
vertically straight tree, 15m high, is broken by the wind in such a way that
its top just touches the ground and makes an angle of $60o$
with the
ground. At what height from the ground did the tree break?

Explanation

To find the height from the ground at which the tree broke, we can follow these steps:

Step 1: Understand the Problem
We have a tree that is 15 meters tall. It breaks and falls such that its top touches the ground, forming an angle of 60 degrees with the ground. We need to find the height from the ground where the tree broke.

Step 2: Set Up the Diagram
Let:
- \( A \) be the point where the tree was originally standing (the top of the tree).
- \( B \) be the point where the tree broke.
- \( C \) be the point where the top of the tree touches the ground.

From the problem, we know:
- The total height of the tree \( AB = 15 \) meters.
- The angle \( \angle ACB = 60^\circ \).

Step 3: Define Variables
Let \( H \) be the height from the ground where the tree broke, i.e., \( H = AB \) (the height from the ground to point B). Therefore, the length \( BC \) (the part of the tree that fell) can be expressed as:
\( BC = 15 - H \)

Step 4: Apply Trigonometric Ratios
In triangle \( ACB \):
- \( AC \) is the hypotenuse (the length of the tree that fell).
- \( AB \) is the opposite side (the height from the ground to the break point).

Using the sine function:
\( AB = AC \cdot \sin(60^\circ) \)

Step 5: Express \( AC \)
From the triangle, we can express \( AC \) in terms of \( H \):
\( AC = 15 - H \)

Step 6: Set Up the Equation
Substituting into the sine equation:
\( H = (15 - H) \cdot \sin(60^\circ) \)
Since \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \):
\( H = (15 - H) \cdot \frac{\sqrt{3}}{2} \)

Step 7: Solve for \( H \)
Rearranging the equation:
\( H = \frac{\sqrt{3}}{2} (15 - H) \)
\( H = \frac{15\sqrt{3}}{2} - \frac{\sqrt{3}}{2}H \)

Bringing all terms involving \( H \) to one side:
\( H + \frac{\sqrt{3}}{2}H = \frac{15\sqrt{3}}{2} \)
\( H(1 + \frac{\sqrt{3}}{2}) = \frac{15\sqrt{3}}{2} \)
\( H = \frac{15\sqrt{3}}{2 + \sqrt{3}} \)

Step 8: Rationalize the Denominator
To simplify \( H \):
Multiply the numerator and denominator by \( 2 - \sqrt{3} \):
\( H = \frac{15\sqrt{3}(2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})} \)
The denominator simplifies to:
\( 2^2 - (\sqrt{3})^2 = 4 - 3 = 1 \)
Thus:
\( H = 15\sqrt{3}(2 - \sqrt{3}) \)

Final Answer
The height from the ground at which the tree broke is:
\( H = 15(2\sqrt{3} - 3) \text{ meters} \)