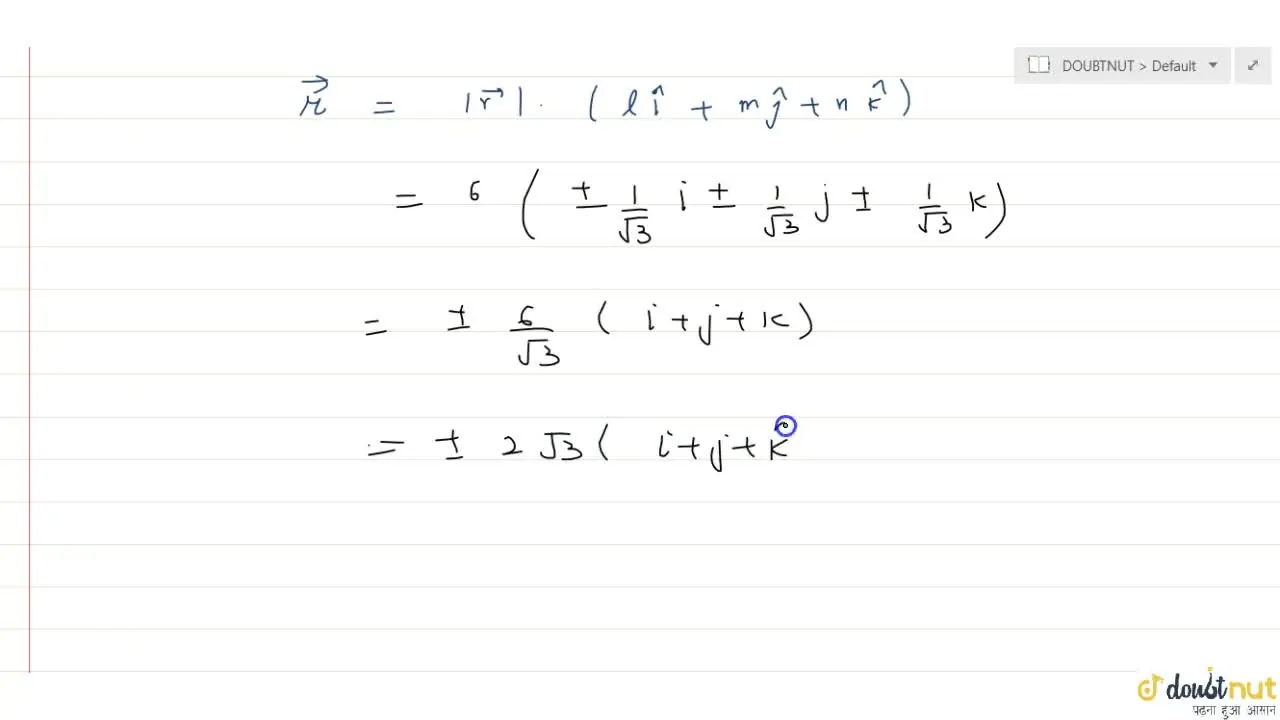A vector →r is inclined at equal acute angles of x−aξs, y−aξs and z−aξs. if |→r|=6 units, find →r.
As the given line is equally inclined with all three coordinate axis,
let it create angle α with all three coordinate axis.
Then,
Direction cosines will be (cosα,cosα,cosα).
∴cos2α+cos2α+cos2α=1
⇒3cos2α=1
⇒cosα=±1√3
Since →r is inclined at acute angle, therefore, cosα=1√3.
Direction cosines will be (1√3,1√3,1√3).
Now, |→r|=6
Therefore, →r=|→r|(lˆi+mˆj+nˆk)
→r=6(1√3ˆi+1√3ˆj+1√3ˆk)
→r=2√3(ˆi+ˆj+ˆk).
Related Playlists
Similar Questions
A vector →r is inclined at equal acute angles of x−aξs, y−aξs and z−aξs. if |→r|=6 units, find →r.
View SolutionThe vector →r is inclined at equal acute angles of x-axis,y axis, and z-axis. If |→r|=6 units, find →r.
View SolutionA vector →r is inclined at equal to OX,OYandOZ. If the magnitude of →r is 6 units, find →r.
View SolutionA vector →r is inclined to x-axis at 450 and y-axis at 600. If |→r|=8 units, find →r.
View SolutionA vector →r is inclined at equal angle to the three axes. If the magnitude of →r is 2√3, find →r.
View SolutionLet →a,→b,→c and are unit vectors inclined to each otherat an angle of 2π3 .If ˆp,ˆqandˆr are unit vectors alongthe angle bisectors of →aand→b,→band→cand→a are spectively, then [ˆpˆqˆr] is equal to
View SolutionTwo vectors →A and →B are inclined to each other at an angle θ. Then a unit vector perpendicular to both →A and →B
View SolutionIf →a,→b and →c are three units vectors equally inclined to each other at an angle α. Then the angle between →a and plane of →band→c is
View SolutionA vector →d is equally inclined to three vectors →a=ˆi+ˆj+ˆk,→b=2ˆi+ˆjand→c=3ˆj−2ˆk. Let→x,→y,and→z be thre vectors in the plane of →a,→b;→b,→c;→c,→a, respectively. Then →x.→d=−1 b. →y.→d=1 c. →z.→d=0 d. →r.→d=0,where→r=λ→x+μ→y+δ→z
View SolutionIf →n is a vector of magnitude √3 and is equally inclined with an acute angle with the coordinate axes. Find the vector and Cartesian forms of the equation of a plane which passes through (2, 1, -1) and is normal to →n .
View Solution