A solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π. Solution in Kannada
The correct Answer is:πcm3
Step by step video, text & image solution for A solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of pi. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE AREAS AND VOLUMES Book:CPC CAMBRIDGE PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:EXERCISE 15.3
Explore 9 Videos
- SURFACE AREAS AND VOLUMES Book:CPC CAMBRIDGE PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:EXERCISE 15.4
Explore 5 Videos
- SURFACE AREAS AND VOLUMES Book:CPC CAMBRIDGE PUBLICATIONChapter:SURFACE AREAS AND VOLUMES Exercise:EXERCISE 15.4
Explore 5 Videos
- STATISTICSBook:CPC CAMBRIDGE PUBLICATIONChapter:STATISTICSExercise:Exercise 13.4
Explore 4 Videos
- TRIANGLESBook:CPC CAMBRIDGE PUBLICATIONChapter:TRIANGLESExercise:Exercise 2.6 (Optional)
Explore 8 Videos
Similar Questions
A metallic sphere of radius 4.2cm is melted and recast into the shape of a cylinder of radius 6cm. Find the height of the cylinder.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14cm . The diameters of its two circular ends. are 4cm and 2cm . Find the capacity of the glass.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14cm . The diameters of its two circular ends. are 4cm and 2cm . Find the capacity of the glass.
View SolutionThe following distribution gives the daily income of 50 workers of a factory.
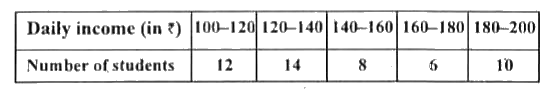
Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
View SolutionIn Fig . PS is the bisecto of ∠QPRofΔPQR . Prove that
QSSR=PQPR
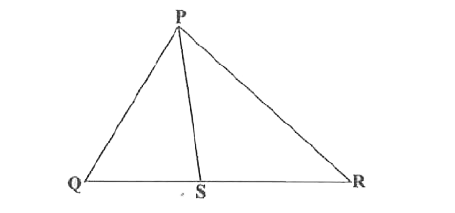
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π .
View SolutionA solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है | इस ठोस का आयतन π के पदों में ज्ञात कीजिए |
View Solutionएक ठोस एक शंकु के आकार का है जो कि एक अर्धगोले पर रखा हुआ है और दोनों की त्रिज्याएँ 1 सेमी हैं तथा शंकु की ऊँचाई इसकी त्रिज्या के बराबर है। इस ठोस का आयतन तथा पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
View Solutionएक ठोस एक अर्द्धगोले के ऊपर समान त्रिज्या 8 सेमी के शंकु के रूप में है और शंकु की ऊंचाई इसकी त्रिज्या के बराबर है ठोस का आयतन ज्ञात कीजिए ।
View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिसकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊंचाई उसकी त्रिज्या के बराबर है । इस ठोस का आयतन π के पदों में ज्ञात कीजिए ।
View SolutionA solid sphere of radius r melted and recast into the shape of a solid cone of height r, then radius of the base of the cone is (of equal volume)
View SolutionA solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of π.
View Solution

