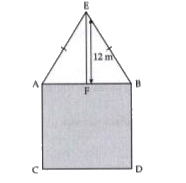
A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m (see Figure). Find its length and breadth.
let length be x m
let breadth be (x−3) m
∠ABC has base = (x−3)m
altitude =12m
area (∠ABC=12×(x−3)×12
=6(x−3)m2
area od DEBC=x×(x−3)
=x2−3xm2
According to question
(x2−3x=4+6(x−3)
x2−3x=4+6x−18
x2−9x+14=0
x2−7x−2x+14=0
x(x−7)−2(x−7)=0
(x−7)(x−2)=0
x=7,2
Case 1 :x=7, length = 7m & breadth=7−3=4m
Case 2 : x=2, length = 2m & breadth =2−3=−1
case 2 cannot be possible
so, length and breadth are 7m&4m
Answer
Related Playlists
- BOOK - NCERTCHAPTER - QUADRATIC EQUATIONSEXERCISE - Exercise 4.12videos
QUADRATIC EQUATIONS
- BOOK - NCERTCHAPTER - QUADRATIC EQUATIONSEXERCISE - EXERCISE 4.311videos
QUADRATIC EQUATIONS
- BOOK - NCERTCHAPTER - QUADRATIC EQUATIONSEXERCISE - EXERCISE 4.26videos
QUADRATIC EQUATIONS
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES13videos
PROBABILITY
- BOOK - NCERTCHAPTER - REAL NUMBERSEXERCISE - EXERCISE 1.33videos
REAL NUMBERS
Similar Questions
A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m (see Figure). Find its length and breadth.
View SolutionA rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m.
What will be the quadratic equation from given information.View SolutionThe area of a rectangular ground is 120m2 and its length is 12 m. Find its breadth.
View SolutionIs it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
View SolutionIs it possible to design or rectangular park of perimeter 40 m and area 400m2? If so, find its length and breadth.
View SolutionIs it possible to design a rectangular park of perimeter 80 m and area 400m2 ? If so, find its length and breadth.
View SolutionIs it possible to design a rectangular park perimetre if 80m and area is 400m2 its length and breadth.
View SolutionThe area of a rectangular ground is 120m2 and its length is 12 m. Find its breadth.
View SolutionThe length of a rectangular field is 8 meters less than twice its breadth.If the perimeter of the rectangular field is 56 meters,find its length and breadth?
View SolutionThe length of a rectangular Field is twice its breadth. If the perimeter of the field is 150 metres. Find its length and breadth.
View Solution


