A point moves such that the sum of the square of its distances from two fixed straight lines intersecting at antle 2α is a constant. The locus of points is an ellipse os eccentricity
√cos2αsinαifα<π4
√−cos2αcosαifα<π4
√cos2αcosαifα<π4
√−cos2αsinαifα<π4
Let us chosse the point of intersection of the givne lines as the origin and their angular bisector as the x-axis. Thenequation of the two lines will bey mx and y=-mx , where = tanα,
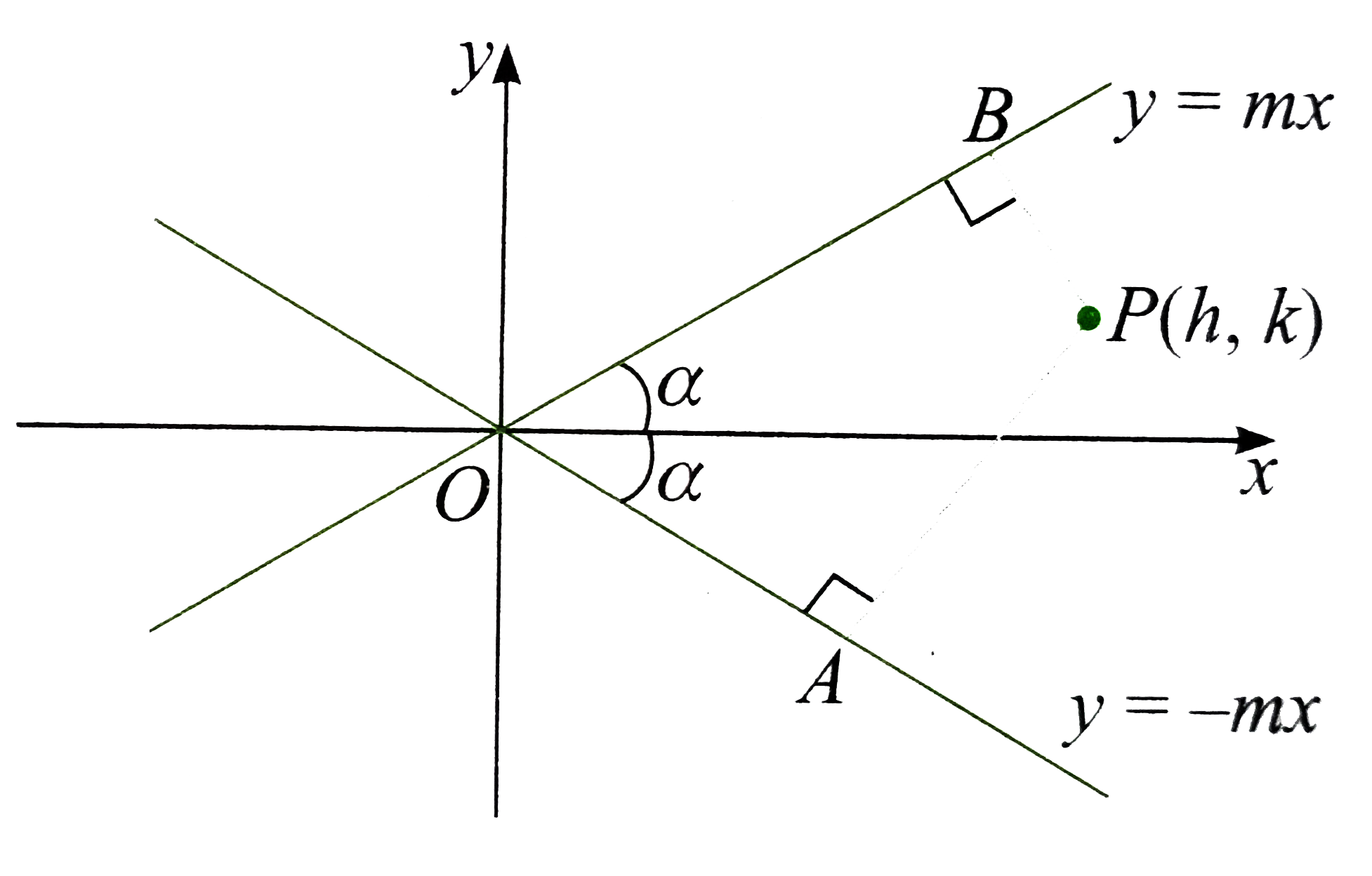
Let P(h,k) be the point whose locus is to be foud.
Then accroding toe the given condition,
PA2+PB2= Constant
⇒(k−mh)21+m2+(k+mh)21+m2 (c is constant)
⇒2(k2+m2h2)=c(1+m2)
Therfore, the locus of pointP is
x2a2+y2b2=1
where a2=c(1+m2)2m2andb2=c(1+m2)2 M
If α<π/4, then m<1,anda2>b2
∴ Ecentricity =√1−b2a2=√1−m2=√cos2αcosα
If α>π/4 then m>1anda2<b2
∴ Ecentricity =√1−b2a2=√1−1m2=√−cos2αsinα
Similar Questions
A point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View SolutionA point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View Solution
Knowledge Check
The locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
AcircleBstraight lineCellipseDnoneThe locus of a point which moves so that the difference of the squares of its distances from two given points is constant, is a
Astraight lineBplaneCsphereDnone of theseThe locus of a point which moves so that the difference of the squares of its distance from two given points is constant, is a
Astraight lineBplaneCsphereDNone of these
A point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point
View SolutionA point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point is
View SolutionA point moves such that the sum of the squares of its distances from the sides of a square of side unity is equal to 9, the locus of such point is
View SolutionThe locus of a point which moves so that the difference of the squares of its distance from two given points is constant, is a
View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
View Solution

