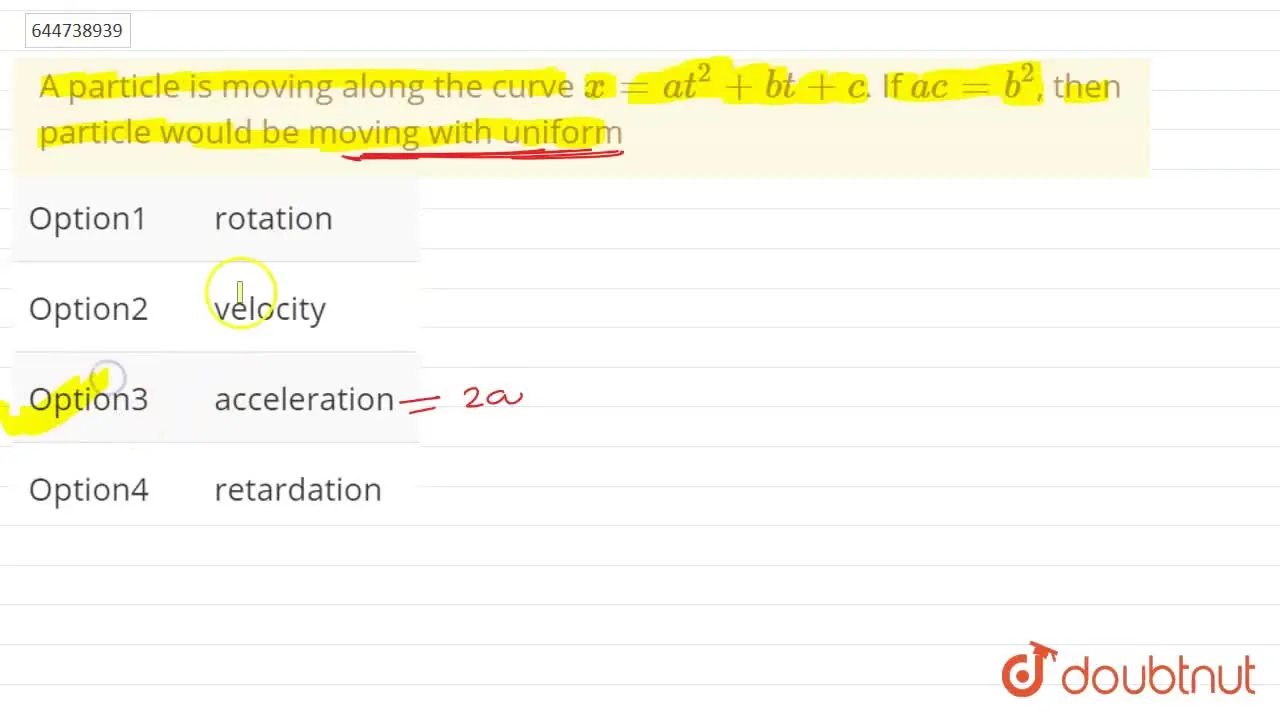
A particle is moving along the curve x=at2+bt+c. If ac=b2, then particle would be moving with uniform
rotation
velocity
acceleration
retardation
The correct Answer is:C
We have,
x=at2+bt+C
⇒dxdt=2at+bandd2xdt2=2a
⇒d2xdt2 = constant.
Related Playlists
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Section I - Solved Mcqs27videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 256videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test30videos
DIFFERENTIAL EQUATIONS
Similar Questions
When a particle moves in a circle with a uniform speed
View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View SolutionA particle is moving along the line 5y=−6x+30 at a rate of 2 units per second. If the particle starts at the y-intercept and moves to the right along this line, how many seconds will it take for the particle to reach the x - axis ?
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionA particle is moving along a circle of radius R with a uniform speed v. At t=0 , the particle is moving along the east. Find the average acceleration (magnitude and direction) in 1/4th revolution.
View SolutionIf a particle is moving along straight line with increasing speed, then
View SolutionA particle moves along the curve y=x2+2x . At what point(s) on the curve are x and y coordinates of the particle changing at the same rate?
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionA particle is moving along a curve 6y=x3+2. Find the points on the curve at which y-coordinate is changing 8 times as fast as the x-coordinate.
View SolutionA particle moves along the curve y=x2+2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
View Solution