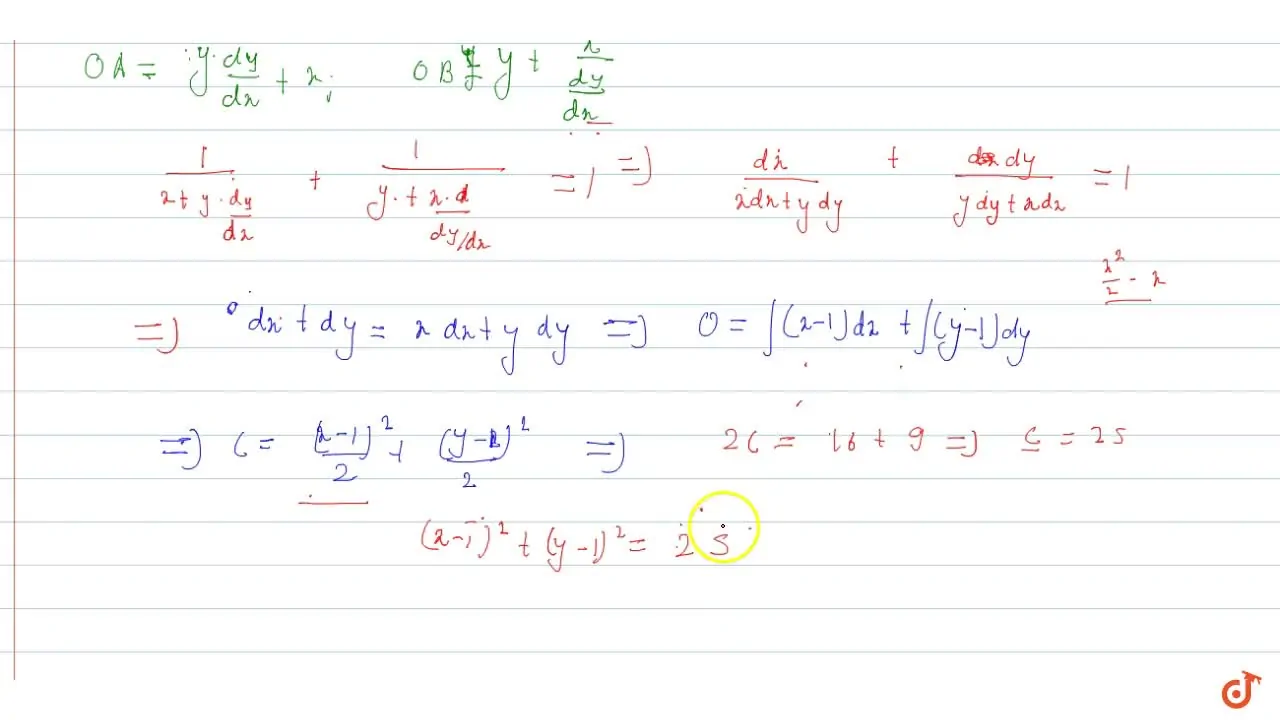A normal is drawn at a point P(x,y) of a curve. It meets the x-axis and the y-axis in point A AND B, respectively, such that 1OA+1OB =1, where O is the origin. Find the equation of such a curve passing through (5.4)
x2+y2−4x−6y+8=0
x2+y2−2x−3y+3=0
2x2+2y2−x−y−2=0
x2+y2−4x+6y−4=0
The correct Answer is:A, D
Equation of normal at P
y′−y=−1m(x−1−x)
A(x+ydydx,0),B(0,y+xdxdy)
2dxxdx+ydy±3dyxdx+ydy=1
2dx+3dy=xdx+ydy
2x+3y=x22+y22+C
C=4
x2−y2−4x−6y+8=0
Related Playlists
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 11videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS9videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS131videos
TEST SERIES
Similar Questions
A normal is drawn at a point P(x,y) of a curve. It meets the x-axis and the y-axis in point A AND B, respectively, such that 1OA+1OB =1, where O is the origin. Find the equation of such a curve passing through (5,4)
View SolutionA normal is drawn at a point A (x, y) of a curve. It meets the X -axis and Y - axis at point P and Q respectively such that 1OP+1OQ=1 where O is the origin. Then, the equation of such a curve passing through (5, 4) is
View SolutionA normal is drawn at a point P(x,y) on a curve. It meets the x-axis and thedus ofthe director such that (x intercept)−1 + (y-intercept)−1=1, where O is origin, the curve passing through (3,3).
View SolutionA normal is drawn at a point P(x, y) of a curve lt meets the x-axis at Q lf PQ is of constant length k such a curve passing through (0,k) is
View SolutionA normal is drawn at a point P(x,y) of a curve. It meets the X-axis at Q. If PQ is of constant length k, then the differential equation describing such a curve is
View SolutionA normal is drawn at a point P (x, y) of a curve. It meets the X- axis at Q. If PQ is of constant length k, then the differential equation describing such a curve is
View SolutionTangent is drawn at any point P of a curve which passes through (1,1) cutting x-axis and y-axis at A and B respectively. If AP:BP=3:1, then,
View SolutionA normal is drawn at a point P(x,y) of a curve. It meets the x-axis at Q. If PQ has constant length k, then show that the differential equation describing such curves is ydydx=±√k2−y2 . Find the equation of such a curve passing through (0,k).
View SolutionA line is drawn from a point P(x,y) on the curve y=f(x), making an angle with the x-axis which is supplementary to the one made by the tangent to the curve at P(x,y). The line meets the x-axis at A. Another line perpendicular to it drawn from P(x,y) meeting the y-axis at B. If OA=OB, where O is the origin, the equation of all curves which pass through (1,1) is
View SolutionIf the length of the sub-normal (projection of that part of the normal which is intercepted between the curve and the x-axis on the x-axis) at any point P on the curve is directly proportional to OP2, where O is the origin, then form the differential equation of the family of curves and hence find the family of curves
View Solution