A line l passing through the origin is perpendicular to the lines l1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk,−∞<t<∞, l2:(3+s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<t<∞ then the coordinates of the point on l2 at a distance of √17 from the point of intersection of l&l1 is/are:
(73,73,53)
(−1,−1,0)
(1,1,1)
(79,79,89)
The correct Answer is:b, d
To solve the problem step by step, we will follow the outlined process based on the given information about the lines l1 and l2, and the conditions provided.
Step 1: Identify the direction vectors of lines l1 and l2
The equations of the lines are given as:
- l1:(3+t)^i+(−1+2t)^j+(4+2t)^k
- l2:(3+s)^i+(3+2s)^j+(2+s)^k
From these equations, we can extract the direction vectors:
- For l1, the direction vector d1=^i+2^j+2^k=(1,2,2)
- For l2, the direction vector d2=^i+2^j+^k=(1,2,1)
Step 2: Find the direction vector of line l
Since line l is perpendicular to both l1 and l2, we can find its direction vector d by taking the cross product of the direction vectors d1 and d2.
d=d1×d2=∣∣
∣
∣∣^i^j^k122121∣∣
∣
∣∣
Calculating the determinant:
d=^i∣∣∣2221∣∣∣−^j∣∣∣1211∣∣∣+^k∣∣∣1212∣∣∣
Calculating each of the minors:
=^i(2⋅1−2⋅2)−^j(1⋅1−1⋅2)+^k(1⋅2−1⋅2)
=^i(2−4)−^j(1−2)+^k(2−2)
=−2^i+1^j+0^k
Thus, the direction vector of line l is (−2,1,0).
Step 3: Find the point of intersection of lines l and l1
Let the point of intersection be M on line l1. The parametric equation of line l through the origin can be expressed as:
M=λ(−2,1,0)=(−2λ,λ,0)
Setting this equal to the coordinates from line l1:
(−2λ,λ,0)=(3+t,−1+2t,4+2t)
This gives us the following equations:
1. −2λ=3+t
2. λ=−1+2t
3. 0=4+2t
From the third equation, we can solve for t:
2t=−4⟹t=−2
Substituting t=−2 into the second equation:
λ=−1+2(−2)=−1−4=−5
Now substituting λ=−5 into the first equation:
−2(−5)=10⟹10=3+t⟹t=7
Step 4: Find the coordinates of point M
Substituting t=−2 back into line l1:
M=(3−2,−1+2(−2),4+2(−2))=(1,−5,0)
Step 5: Find the coordinates of point P on line l2
We need to find point P on line l2 such that the distance PM=√17.
The coordinates of point P on line l2 can be expressed as:
P=(3+s,3+2s,2+s)
Using the distance formula:
PM=√(3+s−1)2+(3+2s+5)2+(2+s−0)2=√17
Squaring both sides:
(3+s−1)2+(3+2s+5)2+(2+s)2=17
This simplifies to:
(2+s)2+(8+2s)2+(2+s)2=17
Expanding and combining like terms:
(2+s)2+(8+2s)2+(2+s)2=4+4s+s2+64+32s+4s2+4+4s+s2=17
6s2+40s+68=17
6s2+40s+51=0
Step 6: Solve the quadratic equation
Using the quadratic formula:
s=−b±√b2−4ac2a=−40±√1600−122412=−40±√37612
=−40±2√9412=−20±√946
Step 7: Find the coordinates of point P
Substituting the values of s back into the equation for P:
1. For s1=−20+√946
2. For s2=−20−√946
Calculating the coordinates for each case will yield the points on line l2 that are at a distance of √17 from point M.
- l1:(3+t)^i+(−1+2t)^j+(4+2t)^k
- l2:(3+s)^i+(3+2s)^j+(2+s)^k
- For l1, the direction vector d1=^i+2^j+2^k=(1,2,2)
- For l2, the direction vector d2=^i+2^j+^k=(1,2,1)
∣
∣∣^i^j^k122121∣∣
∣
∣∣
=^i(2−4)−^j(1−2)+^k(2−2)
=−2^i+1^j+0^k
M=λ(−2,1,0)=(−2λ,λ,0)
(−2λ,λ,0)=(3+t,−1+2t,4+2t)
1. −2λ=3+t
2. λ=−1+2t
3. 0=4+2t
2t=−4⟹t=−2
λ=−1+2(−2)=−1−4=−5
−2(−5)=10⟹10=3+t⟹t=7
M=(3−2,−1+2(−2),4+2(−2))=(1,−5,0)
P=(3+s,3+2s,2+s)
PM=√(3+s−1)2+(3+2s+5)2+(2+s−0)2=√17
(3+s−1)2+(3+2s+5)2+(2+s)2=17
(2+s)2+(8+2s)2+(2+s)2=17
(2+s)2+(8+2s)2+(2+s)2=4+4s+s2+64+32s+4s2+4+4s+s2=17
6s2+40s+68=17
6s2+40s+51=0
s=−b±√b2−4ac2a=−40±√1600−122412=−40±√37612
=−40±2√9412=−20±√946
1. For s1=−20+√946
2. For s2=−20−√946
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE ENGLISHChapter:THREE-DIMENSIONAL GEOMETRY Exercise:ARCHIVES REASONING TYPE
Explore 2 Videos
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE ENGLISHChapter:THREE-DIMENSIONAL GEOMETRY Exercise:ARCHIVES LINKED COMPREHENSION TYPE
Explore 3 Videos
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE ENGLISHChapter:THREE-DIMENSIONAL GEOMETRY Exercise:ARCHIVES SINGLE CORRECT ANSWER TYPE
Explore 9 Videos
- THREE DIMENSIONAL GEOMETRYBook:CENGAGE ENGLISHChapter:THREE DIMENSIONAL GEOMETRYExercise:All Questions
Explore 294 Videos
- TRIGONOMETRIC EQUATIONSBook:CENGAGE ENGLISHChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Matrix Match Type)
Explore 1 Video
Similar Questions
A line l passing through the origin is perpendicular to the lines
1:(3+t)ˆi+(−1+2t)ˆj+(4+2t)ˆk−∞<t<∞and1_(2):(3+2s)ˆi+(3+2s)ˆi+(3+2s)ˆj+(2+s)ˆk,−∞<s<∞
Then the coordinate(s) of the point(s) on 12 at a distance of √17 from the point of intersection of 1 and 11 is (are)
View SolutionFind the equation of a line passing through the point (1,2,3) and perpendicular to the plane →r.(2ˆi−3ˆj+4ˆk)=1.
View SolutionFind the vector equationof the line passing through the point (3,1,2) and perpendicular to the plane →r.(2ˆi−ˆj+ˆk)=4. Find also the point of intersection of this line and the plane.
View SolutionFind the equation of the plane passing through the point ˆi−ˆj+ˆkand perpendicular to the vectro 3ˆi−ˆj−2ˆk and show that the point 2ˆi+4ˆj lies on the plane.
View SolutionFind the equation of a plane passing through origin and which is perpendicular to a normal vector
2ˆi+ˆj−ˆk. (Cartesian form )
View SolutionThe line passing through (-4, -2) and (2, -3) is perpendicular to the line passing through (a, 5) and (2, -1). Find a.
View SolutionFind the equation of the line which passes through the point (-1,3,-2) and is perpendicular to the lines x1=y2=z3 and →r=(−2ˆi+ˆj−ˆk)+λ(−3ˆi+2ˆj+5ˆk).
View SolutionThe area (in square units ) of the triangle formed by y-axis , the straight line L passing through (1,1) and (2,0) and the straight line perpendicular to the line L and passing through (1/2, 0) , is
View SolutionIf a line passing through (−2,1,α) and (4, 1, 2) is perpendicular to the vector 3ˆi−4ˆj+5ˆk and parallel to the plane containing vectors ˆi+2βˆk and 2βˆi+αˆk(∀β≠0), then 10(α+β) is equal to
View Solution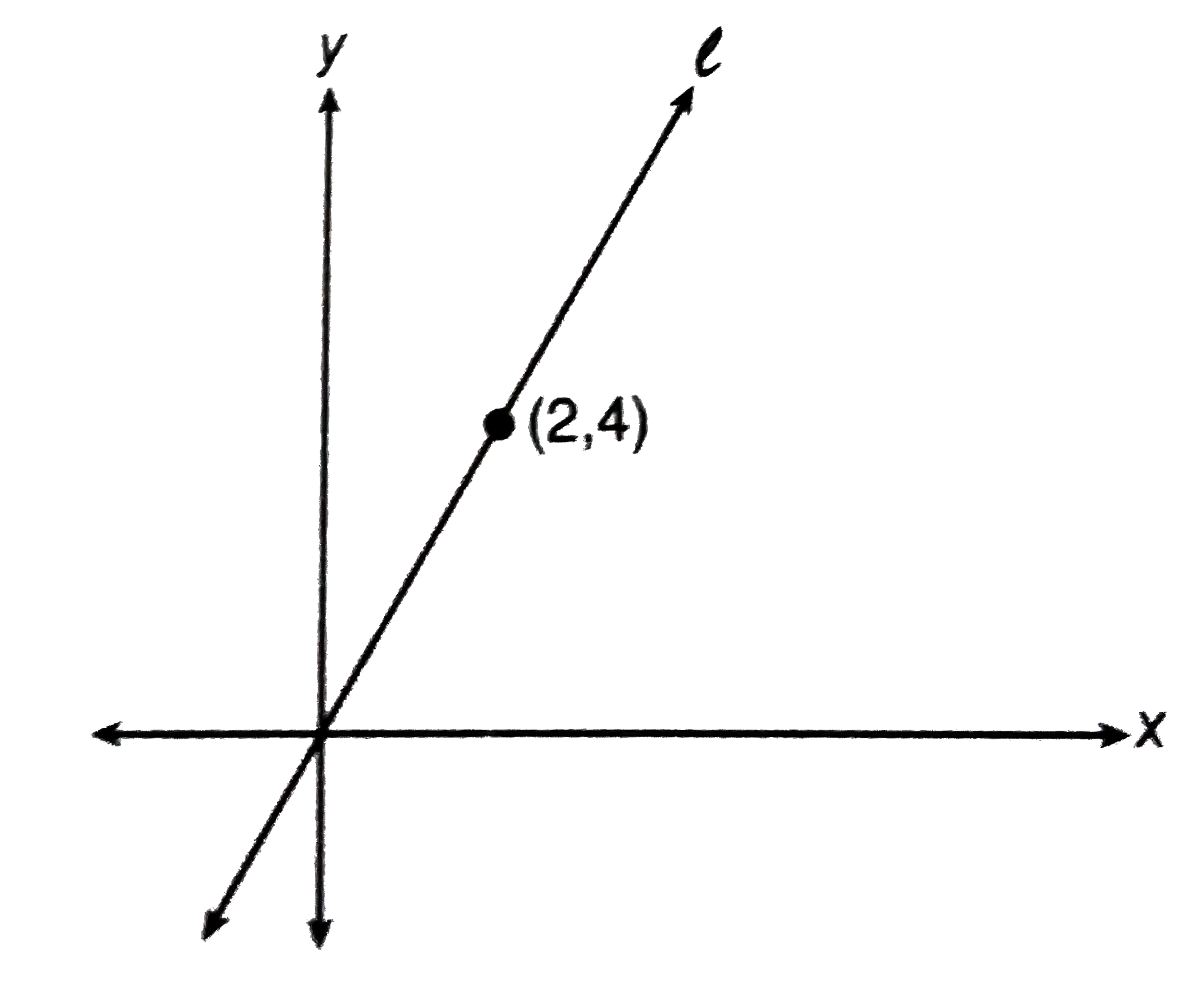
In the accompanying figure. Line l passes through the origin and the point (2, 4). Line m (not shown) is perpendicular to line l at (2, 4). Line m intersects the x-axis at which point?
View Solution

