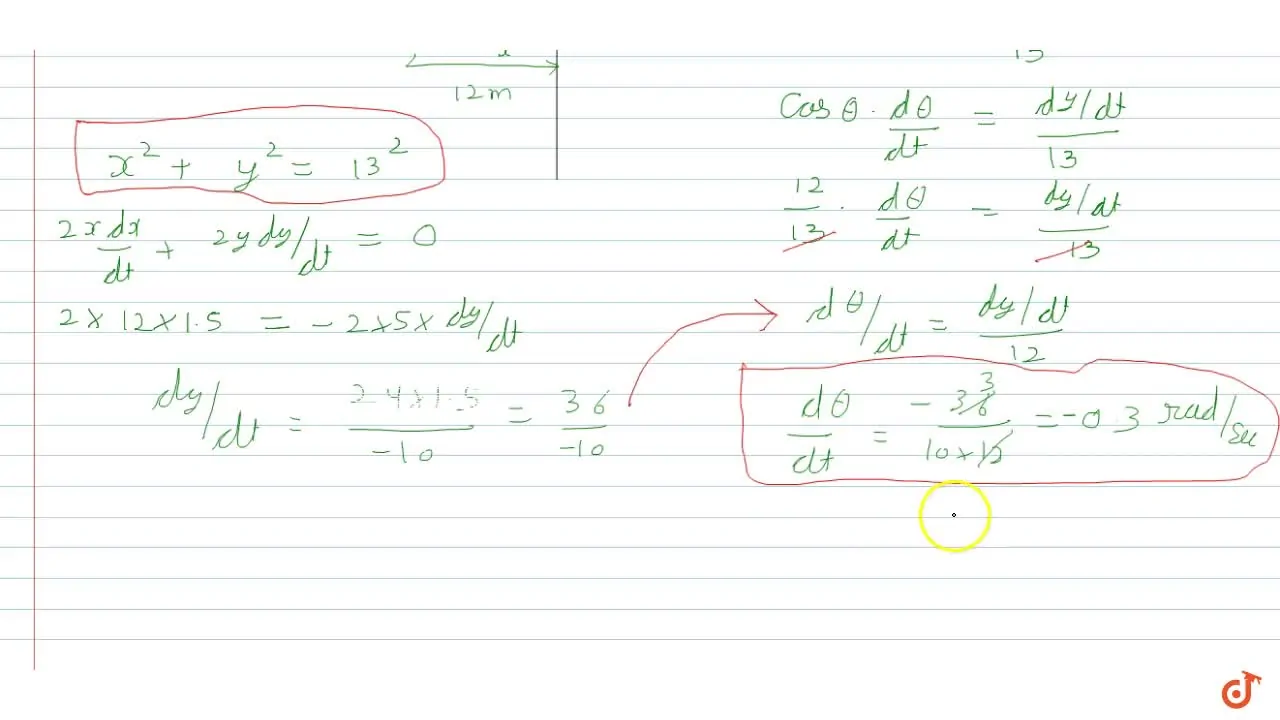A ladder 13m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12m away from the wall.
tanθ=yx
sinθ=y13
differentiating wrt t
cosθ⋅dθdt=dydt13
1213⋅dθdt=dydt13
dθdt=dydt12 eqn (1)
now, x2+y2=132
2xdydt+2ydydt=0
2⋅12⋅1.5=−2⋅5⋅dydt
dydt=24⋅1.5−10=36−10
putting in eqn (1)
dθdt=−3610⋅12=−0.3rad/sec
Related Playlists
Similar Questions
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground,away from the wall at the rate of 10 cm/s. How fast is the angle between the ladder and the ground decreasing when the foot of the ladder is 2 m away from the wall?
View SolutionA ladder 5m long is leaning against a wall. The foot of the ladder is pulled out along the ground away from from the wall at a rate of 2m/s. How fast is the height of ladder on the decreasing at the instant when the foot of the ladder is 4m away from the wall?
View SolutionA ladder 13 m long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall at the rate of 4 m/sec. Find the rate of decreasing at which the top of the ladder moving downwards on wall when the foot of the ladder is 5 m away from the wall.
View SolutionA 13-m long ladder is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 m/s. How fast is its height on the wall decreasing when the foot of the ladder is 5m aways from the wall ?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
View SolutionA ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?
View SolutionA ladder 5 m in length is resting against vertical wall. The bottom of the ladder is pulled along the ground away from the wall at the rate of 1.5m/sec. The length of the highest point of the ladder when the foot of the ladder 4.0 m away from the wall decreases at the rate of
View SolutionA ladder 10 meter long is leaning against a vertical wall. If the bottom of the ladder is pulled horizontally away from the wall at the rate of 1.2 meters per seconds, find how fast the top of the ladder is sliding down the wall when the bottom is 6 meters away from the wall
View SolutionA ladder makes an angle of 30∘ with a wall. If the foot of the ladder is 5 m away from the wall, find the length of the ladder.
View SolutionA ladder 10m long rests against a vertical wall. If the foot of the ladder is 6m away from the wall and the ladder just reaches the top of the wall, how high is the wall?
View Solution