A is the orthocentre of ΔABC and D is reflection point of A w.r.t. perpendicualr bisector of BC, then orthocenter of ΔDBC is :
A
D
B
C
C
B
D
A
Text Solution
The correct Answer is:A
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct15videos
SOLUTION OF TRIANGLES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-3 : Comprehension Type Problems16videos
SOLUTION OF TRIANGLES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)21videos
SEQUENCE AND SERIES
- BOOK - VIKAS GUPTA (BLACK BOOK)CHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems10videos
STRAIGHT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
Aright angledBisoscelesCscaleneDequilateral - Question 2 - Select One
D is a point on the side BC of a ΔABC such that AD bisects ∠BAC . Then
ABD=CDBBA>BDCBD>BADCD>CA - Question 3 - Select One
Let AB be the chord of constant of the point (5, -5) w.r.t the circe x2+y2=5, then the locus of the orthocentre of ΔPAB where P is any point moving on the circle is
A(x−1)2+(y+1)2=5B(x−1)2+(y+1)2=52C(x+1)2+(y−1)2=5D(x+1)2+(y+1)2=52
In triangle ABC,∠A=300,H is the orthocenter and D is the midpoint of BC. Segment HD is produced to T such that HD=DT The length AT is equal to
(a). 2BC
(b). 3BC
(c). 42BC
(d). none of theseView Solutionlocus of point of reflection of point (a,0) w.r.t. the line yt=x+at2 is given by:
View SolutionIn figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
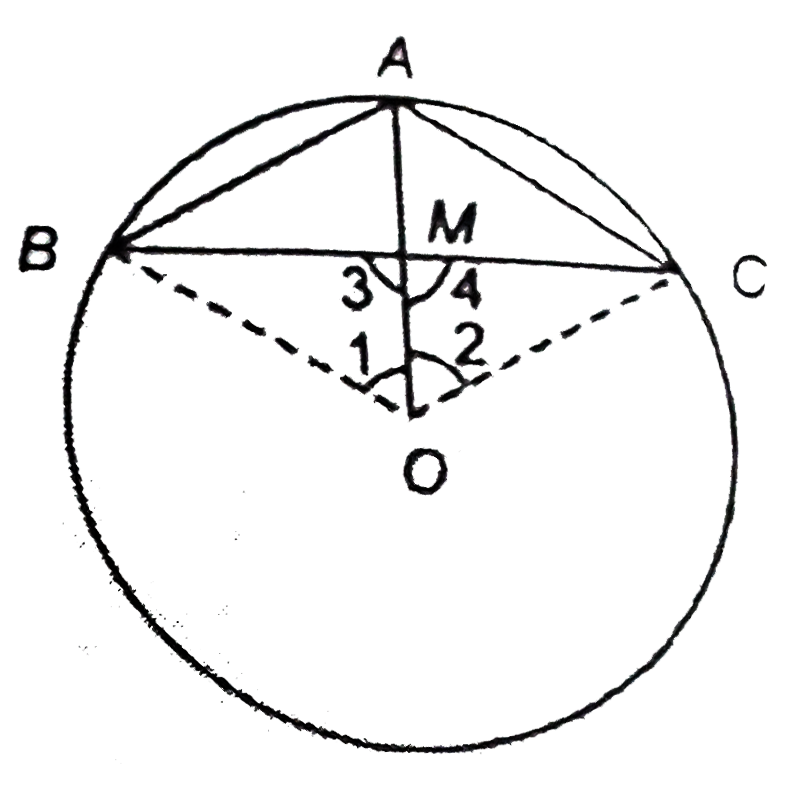
View SolutionIn figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
View SolutionIn ΔABC, the external angle bisector of ∠A is parallel to BC then what is ΔABC?
View Solution