A function f:R→R satisfies the equation f(x+y)=f(x)f(y),∀x,y in R and f(x)≠0 for any x in R . Let the function be differentiable at x = 0 and f'(0) = 2. Show thatf'(x)=2f(x),∀x in R. Hence, determine f(x)
The correct Answer is:e2x
We have, f(x+y)=f(x)⋅f(y),∀x,y∈R.
∴F(0)=f(0)⋅f(0)⇒f(0){f(0)−1}=0
⇒ f(0)=1 [∵f(0)≠0]
Since, f'(0)=2⇒limh→0f(0+h)−f(0)h=2
⇒ limh→0f(h)−1h=2 [∵f(0)=1] ....(i)
Also, f'(x)=limh→0f(x+h)−f(x)h
=limh→0f(x)⋅f(h)−f(x)h ,
[using, f(x+y)=f(x)⋅f(y)]
=f(x){limh→0f(h)−1h}
∴ f'(x)=2f(x) [from Eq. (i)]
⇒ f'(x)f(x)=2
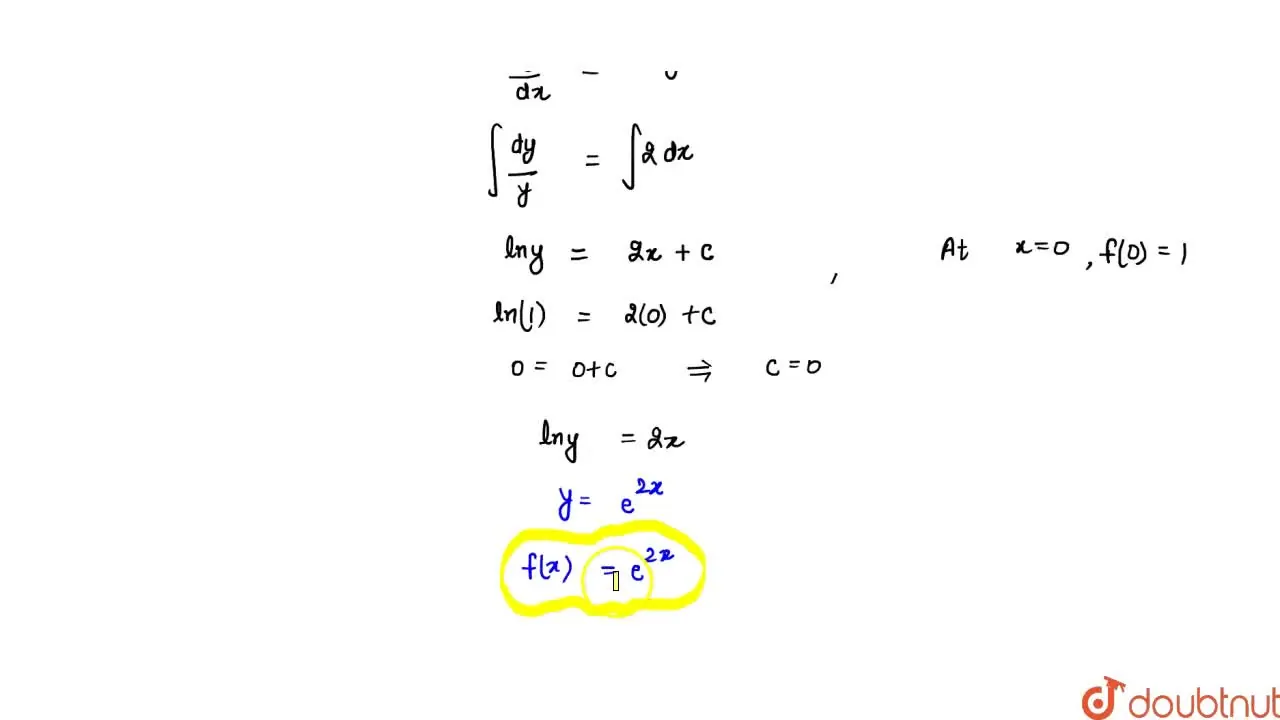
On integrating both sides between 0 to x, we get
∫x0f'(x)f(x)dx=2x
⇒ loge∣f(x)−loge|f(0)|=2x
⇒ loge|f(x)|=2x [∵f(0)=1]
⇒ loge|f(0)|=0
⇒ f(x)=e2x
Related Playlists
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point (Integer Answer Type Questions)3videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiation (Objective Questions I)20videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - LIMIT,CONTINUITY AND DIFFERENTIABILITY EXERCISE - Differentiability at a point (True/False)1videos
LIMIT,CONTINUITY AND DIFFERENTIABILITY
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - JEE MAINSEXERCISE - All Questions1videos
JEE MAINS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - MATRICES AND DETERMINANTSEXERCISE - SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)2videos
MATRICES AND DETERMINANTS
Similar Questions
A function f:R→R satisfy the equation f(x).f(y)=f(x+y) for all x,y∈R and f(x)≠0 for any x∈R. Let the function be differentiable at x = 0 and f'(0)=2, Then :
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x).f(y) for all xy∈R,f(x)≠0. Suppose that the function is differentiable at x=0 and f'(0)=2, then prove that f'=2f(x).
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for all values of x and y and for any x∈R,f(x)≠0. Suppose the function is differentiable at x=0 and f' (0) = 2, then for all x∈R,f(x)=
View SolutionConsider a function f :R →R which satisfies the equation f (x + y ) = f (x ) . f (y ), ∀ x, y ∈ R, f (x )≠ 0. Suppose that the function is differentiable at x = 0 and f'(0) = 2. Then, f (x ) is equal to
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x).f(y) for all, f(x)≠0. Suppose that the function is differentiable at x = 0 and f'(0) = 2. Then,
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for all values of x and y and for any x∈R,f(x)≠0. Suppose the function is differentiable at x=0 and f'(0)=2, then for all x∈R,f(x)=
View SolutionA function f(x) satisfies the relation f(x+y)=f(x)+f(y)+xy(x+y),∀x,y∈R. If f'(0) = - 1, then
View SolutionA function f:R→R satisfies that equation f(x+y)=f(x)f(y) for all x, y∈R , f(x)≠0 . Suppose that the function f(x) is differentiable at x=0 and f′(0)=2 . Prove that f′(x)=2 f(x) .
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for allx,y∈R and f(x)≠0 for all x∈R. If f(x) is differentiable at x=0andf′(0)=2, then prove that f′(x)=2f(x).
View SolutionA function f:R -> R satisfies the equation f(x+y)=f(x)f(y) for all x,y∈R.f(x)≠0 Suppose that the function is differentiable at x=0 and f′(0)=2. Prove that f′(x)=2f(x).
View Solution