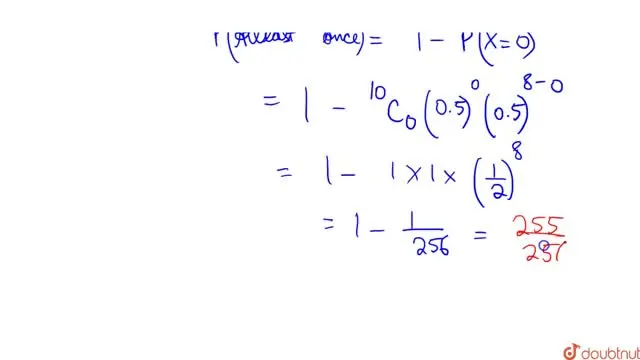A fair coin is tossed 8 times. Find the probability that it shows heads
(i) exactly 5 times (March ' 17)
(2) at lest once . (March ' 14- 17 )
Given : X = number of heads
p = probability of getting head
∴p12
∴q=1−p=1−12=12
Given , n= 8
∴X~B(8,12)
The p.m f of X is given as
P(X=x)=pp(x)=nCxPxqn−x
i.e P(x)=8Cx(12)x(12)8−5
=8C3(12)5(12)3 ltbr gt =8×7×61×2×3×1256=732
∴P[X=5]=0.21875
Hence , the probability of getting exactly 5 heads is 0.21875.
(2) P ( getting heads at lest once )
=[X≥1]=1−P[x=0]
1−p(0)=1−8C0(12)0(12)8−0
1−(12)8=1−1256=2555256
∴p[X≥1]=0.996
Hence , the probability of getting heads at least once is 0.996.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - Examples for practice16videos
BINOMIAL DISTRIBUTION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS8videos
BINOMIAL DISTRIBUTION
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - APPLICATIONS OF DERIVATIVES EXERCISE - MULTIPLE CHOICE QUESTIONS12videos
APPLICATIONS OF DERIVATIVES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CONTINUITY EXERCISE - MULTIPLE CHOICE QUESTIONS6videos
CONTINUITY
Similar Questions
A fair coin is tossed 9 times . Find the probability that it shows heads exactly 5 times .
View SolutionA fiar coin is tossed 18 times. Find the probability that it shows least once.
View SolutionFive fair coins are tossed 8 times, then the probability that it shows heads exactly 5 times is
View SolutionA fair coin is tossed 5 times . Find the probability that it shows exactly three times head.
View SolutionIf a fair coin is tossed 8 times , then the probability that it shows heads at least once is
View SolutionA fair coin is tossed 12 times. Find the probability that two heads do not occur consectively.
View SolutionA coin is tossed 6 times . Find the probability of getting at least 3 heads .
View SolutionA Fair coin is tossed 5 times , find the probability that a) coin shows exactly three times head b) no head.
View SolutionA coin is tossed two times. Find the probability of getting atmost one head.
View SolutionA fair coin is tossed 8 times. Find the probability that :
(1) it shows no head
(2) it shows head at least once.View Solution