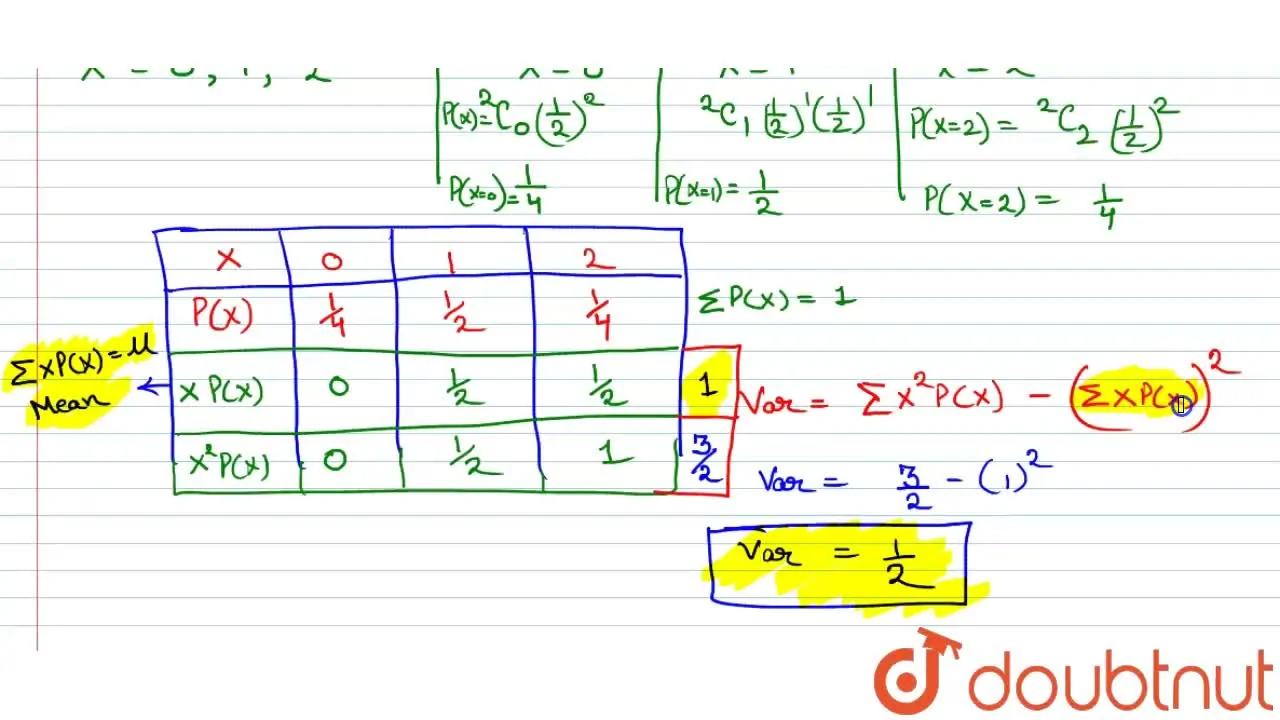
A die is tossed twice . If a success is getting an even number on a toss , then find the variance of the number of successes .
Let X be the random variable for a success for getting an even number on a toss .
∴ X=0,1,2,n=2,p=32=12 and q = 12
At X = 0 , P(X=0)=2C0(12)0(12)2−0=14
At X = t , P(X=1)=2C0(12)1(12)2−1=2⋅12⋅12=12
At X = 2 , P(X=2)=2C2(12)2(12)2−2=14

∴ ∑XP(X)=0+12+12=1 .....(i)
and ∑X2P(X)=0+12+1=32 .....(ii)
∵ Var(X) = E(X2)−[E(X)]2
=∑X2P(X)−[∑XP(X)]2=32−(1)2=12 [using Eqs. (i) and (ii)]
Related Playlists
Similar Questions
A die is tossed twice A success is getting an odd number on a toss. Find the variance of the number of successes.
View SolutionA die is tossed thrice. A success is getting 5 or 6 on a toss. The mean and the variance of number of successes
View SolutionA die is thrown thrice. A success is or 6 in a throw. Find the mean and variance of the number of successes.
View SolutionA die is thrown 100 times. If getting an even numebr is considered a success, the variance of the number of successes, is
View SolutionA die is thrown 100 times, getting an even number is considered a success. The variance of the number of successes is
View SolutionA die is thrown 100 times, getting an even number is considered a success. The variance of the number of successes is
View SolutionA die is thrown 100 times, getting an even number is considered a success. The variance of the number of successes is
View SolutionA die is thrown 100 times, getting an even number is considered a success. The variance of the number of successes is
View SolutionA die is rolled 20 times . Getting a number greater than 4 is a success.
Find the mean and variance of the number of successes .View SolutionA die is tossed thrice. If event of getting an even number is a success. Then the probability of getting at least two successes is
View Solution