A circle of radius 4 cm is inscribed in ΔABC, which touches side BC at D. If BD = 6 cm, DC = 8 cm then
the triangle is necessarily acute angled
tan.A2=47
perimeter of the triangle ABC is 42 cm
area of ΔABC is 84cm2
The correct Answer is:A, B, C, D
To solve the problem step by step, we will follow the logical progression outlined in the video transcript.
1. Draw the Triangle and Identify Points:
- Draw triangle ABC with an inscribed circle that touches side BC at point D.
- Label the lengths: BD = 6 cm and DC = 8 cm.
2. Calculate Length of Side BC:
- Since BD + DC = BC, we can calculate:
BC=BD+DC=6 cm+8 cm=14 cm
3. Identify the Inradius (r):
- The radius of the inscribed circle (inradius) is given as r = 4 cm.
4. Use the Incenter Angles:
- Let I be the incenter of triangle ABC. The angles at I are related to the angles of triangle ABC:
- ∠IBD=B2
- ∠ICD=C2
5. Calculate Tangents:
- Using the tangent definitions:
tan(B2)=rBD=46=23
tan(C2)=rDC=48=12
6. Use the Formula for Tangents:
- We use the formula for the product of tangents:
tan(B2)tan(C2)=√(s−a)(s−b)s(s−c)
- Here, s is the semi-perimeter of the triangle.
7. Calculate the Semi-perimeter (s):
- The semi-perimeter s is given by:
s=AB+AC+BC2
- We need to express s in terms of a, b, and c. We know BC=a=14 cm.
8. Set Up the Equation:
- Let b=AB and c=AC. We can express the tangents:
23⋅12=√(s−a)(s−b)s(s−c)
- Simplifying gives:
13=√(s−14)(s−b)s(s−c)
9. Substituting Values:
- We know s=AB+AC+142. We can solve for s using the area formula.
10. Calculate Area of Triangle:
- The area A of triangle ABC can be calculated using:
A=r⋅s
- We already know r=4 cm. We need to find s first.
11. Final Calculation:
- From the previous steps, we can find s to be 21 cm.
- Therefore, the area is:
A=4⋅21=84 cm2
Final Answer:
The area of triangle ABC is 84 cm2.
- Draw triangle ABC with an inscribed circle that touches side BC at point D.
- Label the lengths: BD = 6 cm and DC = 8 cm.
- Since BD + DC = BC, we can calculate:
BC=BD+DC=6 cm+8 cm=14 cm
- The radius of the inscribed circle (inradius) is given as r = 4 cm.
- Let I be the incenter of triangle ABC. The angles at I are related to the angles of triangle ABC:
- ∠IBD=B2
- ∠ICD=C2
- Using the tangent definitions:
tan(B2)=rBD=46=23
tan(C2)=rDC=48=12
- We use the formula for the product of tangents:
tan(B2)tan(C2)=√(s−a)(s−b)s(s−c)
- Here, s is the semi-perimeter of the triangle.
- The semi-perimeter s is given by:
s=AB+AC+BC2
- We need to express s in terms of a, b, and c. We know BC=a=14 cm.
- Let b=AB and c=AC. We can express the tangents:
23⋅12=√(s−a)(s−b)s(s−c)
- Simplifying gives:
13=√(s−14)(s−b)s(s−c)
- We know s=AB+AC+142. We can solve for s using the area formula.
- The area A of triangle ABC can be calculated using:
A=r⋅s
- We already know r=4 cm. We need to find s first.
- From the previous steps, we can find s to be 21 cm.
- Therefore, the area is:
A=4⋅21=84 cm2
The area of triangle ABC is 84 cm2.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Linked comprehension type
Explore 34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Matrix match type
Explore 6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercises
Explore 80 Videos
- PROGRESSION AND SERIESBook:CENGAGE ENGLISHChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Archives(Matrix Match Type)
Explore 1 Video
Similar Questions
Knowledge Check
In quadrilateral ABCD angled D=90∘, BC=38cm and DC=25cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB=27cm. Find the radius of the circle.
A28cmB14cmC35cmD19cm
In Fig. 2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB=29 cm, AD-23 cm,∠B=90° and DS = 5 cm, then the radius of the circle (in cm)
View SolutionConstruct a ΔABC right angled at B in which BC = 6.0 cm and AC = 8.0 cm.
View SolutionIn Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
View SolutionConstruct a ΔABC in which AB = 4 cm, BC = 5.2 cm and CA = 4.5 cm.
View SolutionIn the following figure, a circle is inscribed in th equadrilaterial ABCD.
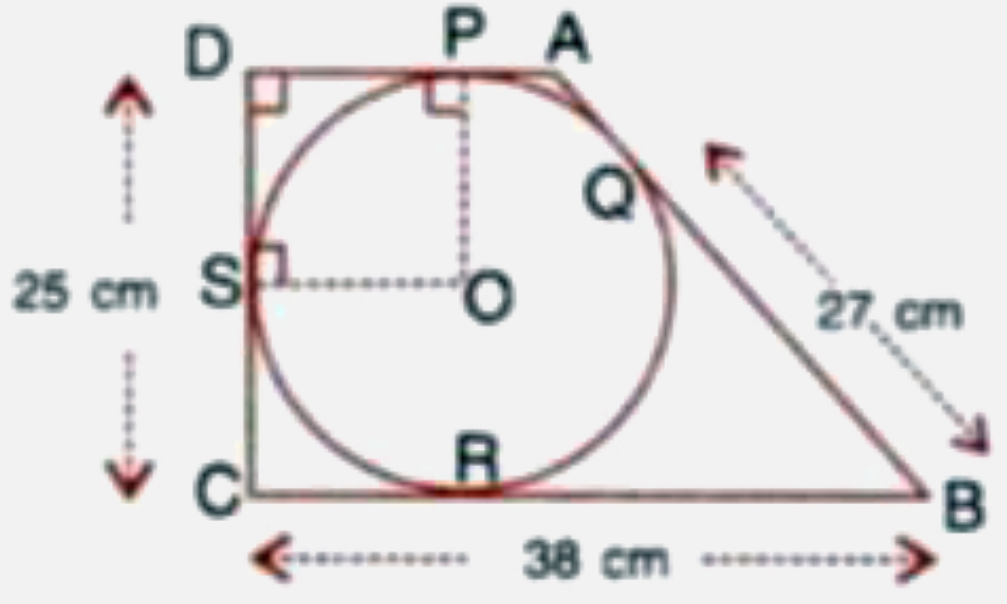 width="80%">
width="80%">
If BC=38 cm, QB=27cm, DC=25 cm and that AD is perpendicular to DC, find the radius of the circle.
View Solution

