A box contains 16 bulbs, out of which 4 bulbs are defective. Three bulbs are drawn at random from the box. Let X be the number of defective bulbs drawn. Find the mean and variance of X.
The correct Answer is:Mean =34,variance =3980
Three bulbs drawn one by one without replacement is the same as drawing 3 bulbs simultaneously.
Let X = number of defective bulbs in a lot of 3 bulbs drawn.
Then, X=0,1,2 or 3.
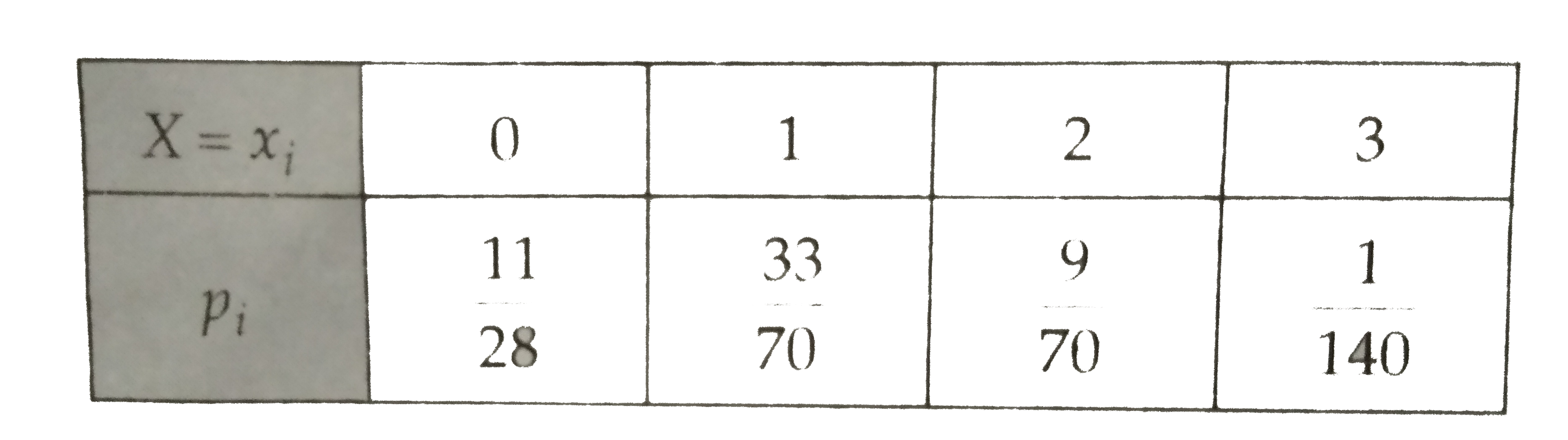
P(X=0)=P(one of the bulbs is defective)
=12C316C3=(12×11×103×2×1×3×2×116×15×14)=1128.
P(X=1)=P(1 defective bulb and 2 nondefective bulbs)
4C1×12C216C3=(4×12×112×1×3×2×116×15×14)=3370.
P(X=2)=P(2 defective bulbs and 1 nondefective bulb)
=(4C2×12C1)16C3=(4×32×1×12×3×2×116×15×14)=970.
P(X=3)=P(3 defective bulbs)
=4C316C3=(4×3×23×2×1×3×2×116×15×14)=1140.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Objective Questions30videos
PROBABILITY DISTRIBUTION
- BOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 3232videos
PROBABILITY DISTRIBUTION
- BOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 3232videos
PROBABILITY DISTRIBUTION
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B2videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions34videos
PRODUCT OF THREE VECTORS
Similar Questions
Three defective bulbs are mixd with 7 good ones. Let X be the number of defective bulbs when 3 bulbs are drawn at random. Find the mean and variance of X.
View SolutionFour rotten oranges are accidentally mixed with 16 good ones. Three oranges are drawn at random from the mixed lot. Let X be the number of rotten oranges drawn. Find the mean and variance of X.
View SolutionA box contains 16 bulbs out of which 4 bulbs are defective. 3 bulbs are drawn one by one from the box without replacement. Find the probability that all three are defective bulbs
View SolutionA box contains 13 bulbs out of which 5 bulbs are defective. 3 bulbs are drawn one by one from the box without replacement. Find the probability that exactly 2 bulbs are defective.
View SolutionThere are 3 defective bulbs, in a group of 10 bulbs. If X is the number of defective bulbs in a random draw of 3 bulbs, then find its mean and variance.
View SolutionA box contains 100 bulbs out of which 10 are defective. A sample of 5 bulbs is drawn. The probability that none is defective , is
View SolutionA box contains 100 bulbs , out of which 10 are defective. A sample of 5 bulbs is drawn. The probability that none is defective ,is
View SolutionA lot of 25 bulbs contain 5 defective ones. One bulb is drawn at random from the lot. What is the probability that the bulb is good.
View SolutionA lot of 20 bulbs contains 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
View SolutionFrom a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
View Solution


