AB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
We have, AB=2r
and ∠ACB=90∘ [since, angle in the semi-circle is always 90∘]
Let AC=x and BC=y
∴(2r)2=x2+y2
⇒y2=4r2−x2
⇒y=√4r2−x2 ……………………(i)
Now, area of ΔABC,A=12×x×y
=12×x×(4r2−x2)1/2 [using Eq. (i)]
Now, differentiating both sides w.r.t. x, we get
dAdB=12[x.12(4r2−x2)−12.(0−2x)+(4r2−x2)1/2.1]
=12[(−2x)22√4r2−x2+(4r2−x2)1/2]
12[−x2√4r2−x2+√4r2−x2]
=12[−x2+4r2−x2√4r2−x2]=12[−2x2+4r2√4r2−x2]
⇒dAdx=[−x2+2r2√4r2−x2]
Now, dAdx=0
⇒−x2+2r2=0
⇒r2+12x2
⇒r=1√2x2
∴x=r√2x

Again, differentiating both sides, w.r.t. x, we get
d2Adx2=√4r2−x2.(−2x)+(2r2−x2).12(4r2−x2)1/2(−2x)√4r2−x22
=−4x(√4r2−x2)+(2r2−x2)(−2x)2.(4r2−x2)3/2
=−4x(4r2−x2)+(2r2−x2).(−2x)2.(4r2−x2)3/2
=−16xr2+4x3+(2r2−x2)(−2x)2.(4r2−x2)3/2
d2A(dx2)x=r√2=−16.r√2.r2+4.(r√2)3+[2r2−(r√2)2].(−2.r√2)2.(4r2−2r2)3/2 [∴x=r√2]
=16.√2.r3+8√2r32(2r2)3/2=8√2r2[r−2]4r3
=−8√2r34r3=−2√2<0
For x=r√2, the area of triangle is maximum.
For x=r√2, y=√4r2−(r√2)2=√2r2=r√2
Since, x=r√2=y
Hence, the triangle is isosceles.
Related Playlists
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - OBJECTIVE TYPES QUESTIONS25videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers5videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers5videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions22videos
APPLICATION OF INTEGRALS
Similar Questions
AB is a diameter of a circle and C is any point on the circumference of the circle. Then a) the area of ABC is maximum when it is isosceles b) the area of ABC is minimum when it is isosceles c) the perimeter of ABC is minimum when it is isosceles d) none of these
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then (a) the area of ΔABC is maximum when it is isosceles (b) the area of ΔABC is minimum when it is isosceles (c) the perimeter of ΔABC is minimum when it is isosceles (d) none of these
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIn the figure, A, B, C are points on the circle. What is the value of x?
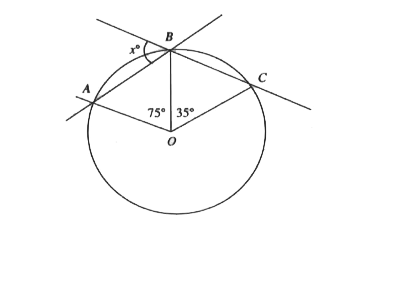 View Solution
View SolutionIn figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
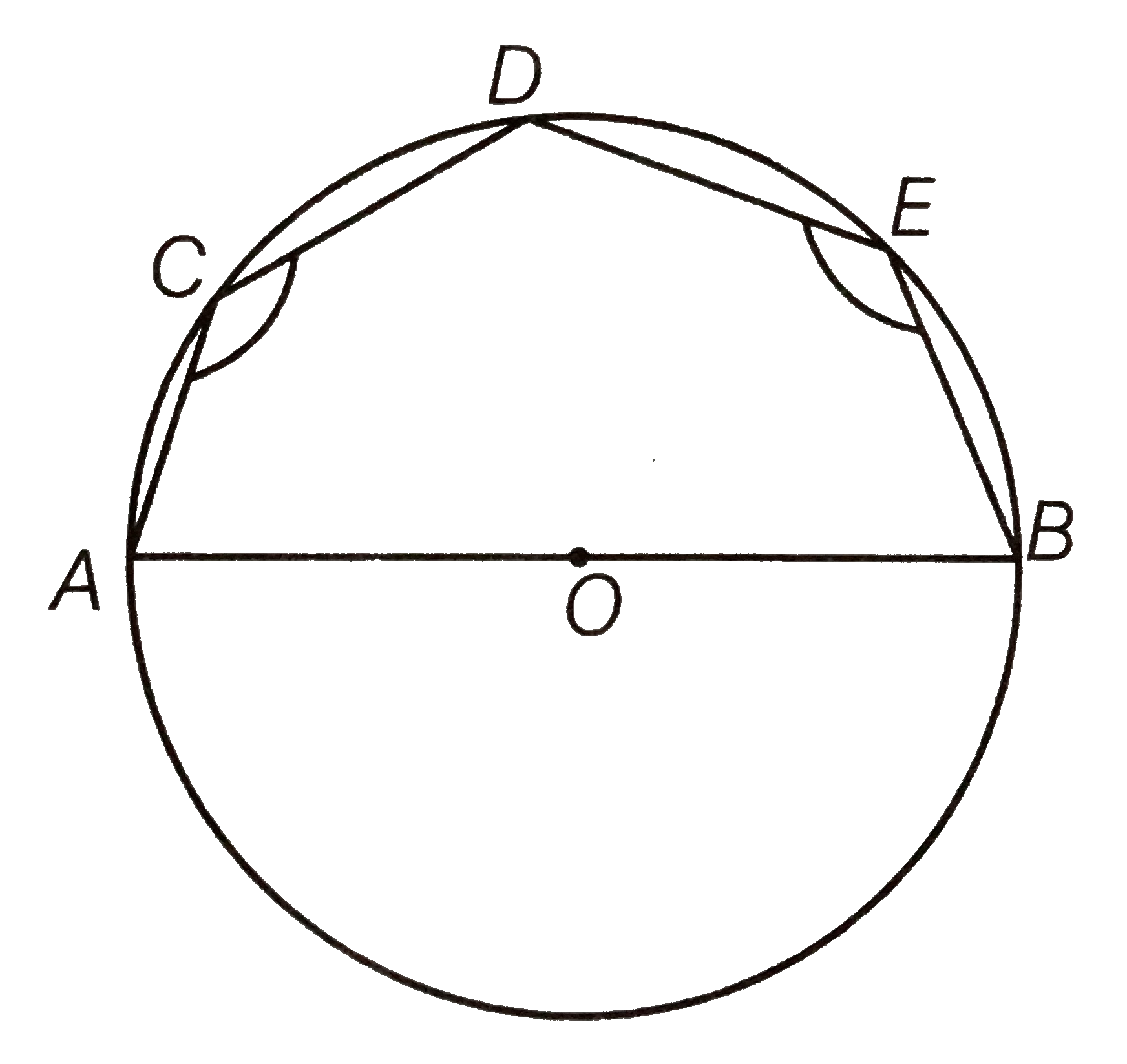 View Solution
View SolutionAn isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a . Show that the area of the triangle is maximum when θ=π6 .
View SolutionThe sum of the perimeters of a square and a circle is given. Show that the sum of their areas is minimum when the length of a side of the square is equal to the diameter of the circle.
View Solution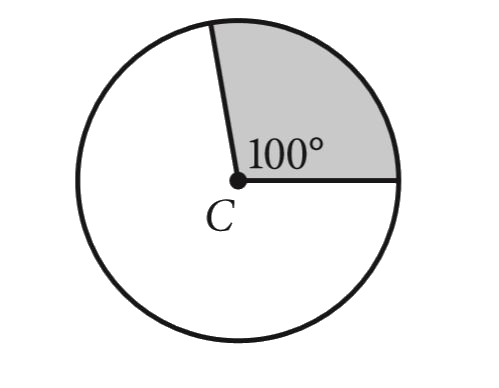
Point C is the center of the circle above. What fraction of the area of the circle is the area of the shaded region?View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC then,
View SolutionIn Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
View Solution


