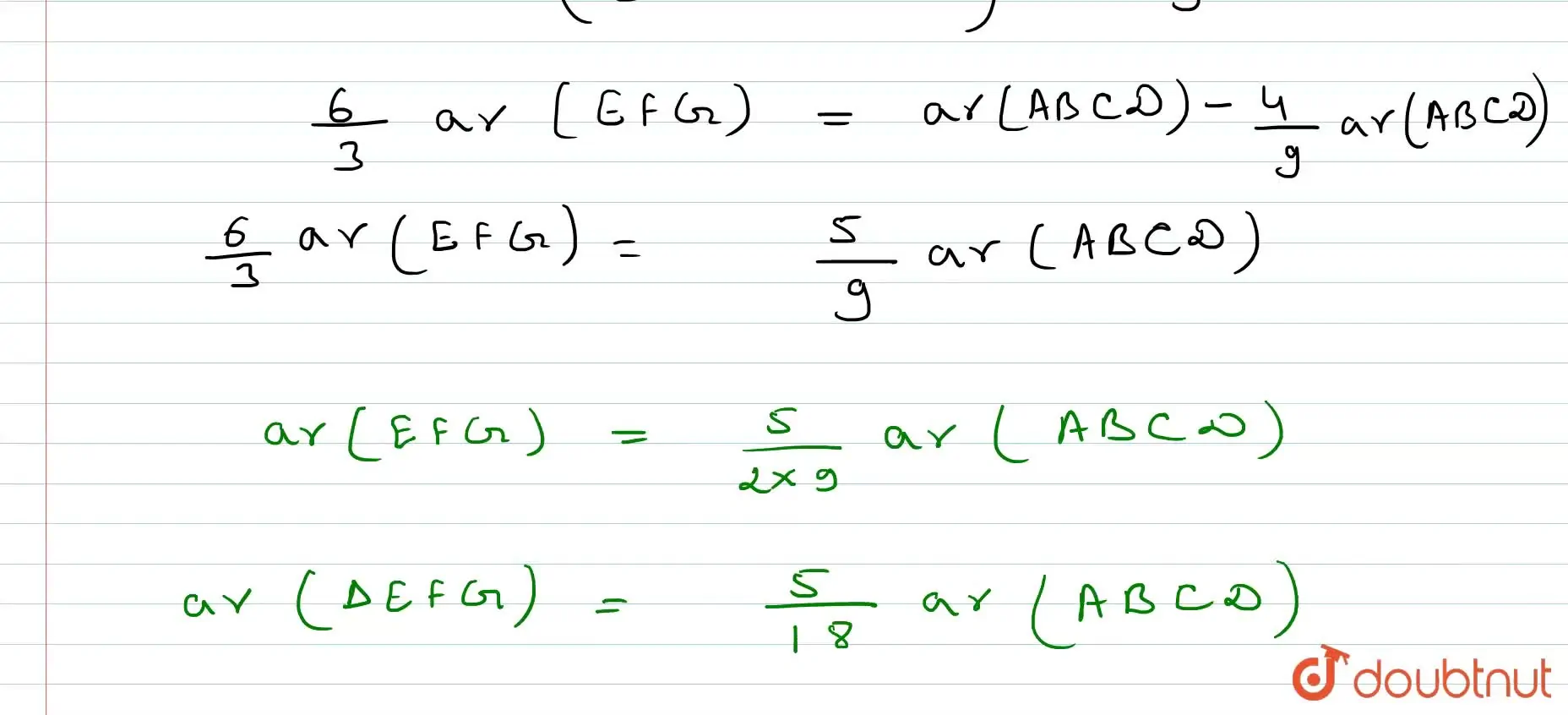ABCD is a parallelogram, G is the point on AB such that AG=2GB ,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: Find what portion of the area of parallelogram is the area of EFG
ar(△EFG)=ar(trap. BGEC)-ar(△BGF)
Now, ar(trap. BGEC)=12(GB+EC)×EP
12(13AB+23CD)×EP
12AB×EP
12ar(∣∣gmABCD)
ar(△BGF)=12×BF×GR
12×23BC×GR
23×12BC×GR
23×ar(△GBC)
23×12GB×EP
13×13AB×EP
19AB×EP
19ar(∣∣gmABCD)
ar(△EFG)=12
ar(∣∣gmABCD)−19ar(∣∣gmABCD)−19ar(∣∣gmABCD)
518ar(||gm ABCD)
Related Playlists
Similar Questions
ABCD is a parallelogram, G is the point on AB such that AG=2GB ,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: Find what portion of the area of parallelogram is the area of EFG
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: arEGB=16ar(ABCD)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View Solution