किनारे वाले के घन को किनारे वाले कितने घनों में विभक्त किया जा सकता है
The correct Answer is:D
Step by step video, text & image solution for 5 cm किनारे वाले के घन को 1 cm किनारे वाले कितने घनों में विभक्त किया जा सकता है ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - EXERCISE - 15 (लघु उत्तरीय प्रश्न )10videos
पृष्ठीय क्षेत्रफल और आयतन
- BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - EXERCISE - 15 ( दीर्घ उत्तरीय प्रश्न )12videos
पृष्ठीय क्षेत्रफल और आयतन
- BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - वस्तुनिष्ठ प्रश्न7videos
पृष्ठीय क्षेत्रफल और आयतन
- BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - बहुविकल्पीय प्रश्न14videos
निर्देशांक ज्यामिति
- BOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - दीर्घ उत्तरीय प्रश्न3videos
प्रायिकता या सम्भावित
Similar Questions
पानी का एक हौज 4 m लम्बा ,3.5m चौड़ा है और हौज पानी से भरा है । पानी की सतह को 2 cm नीचा करने के लिए कितना घन सेमी पानी निकालना होगा ?
03:21View Solution8 cm किनारे वाले दो घन बराबर से जोड़ दिये गये है। परिणामी घनाभ का पृष्ठ क्षेत्रफल ज्ञात करें।
04:18View Solutionयदि a,b,c आयाम वाले किसी घनाभ का आयतन V और पृष्ठ - क्षेत्रफल S हो , तो 2S(1a+1b+1c) बराबर है
02:28View Solutionबगल के चित्र में , बिंदु A के निर्देशांक हैं
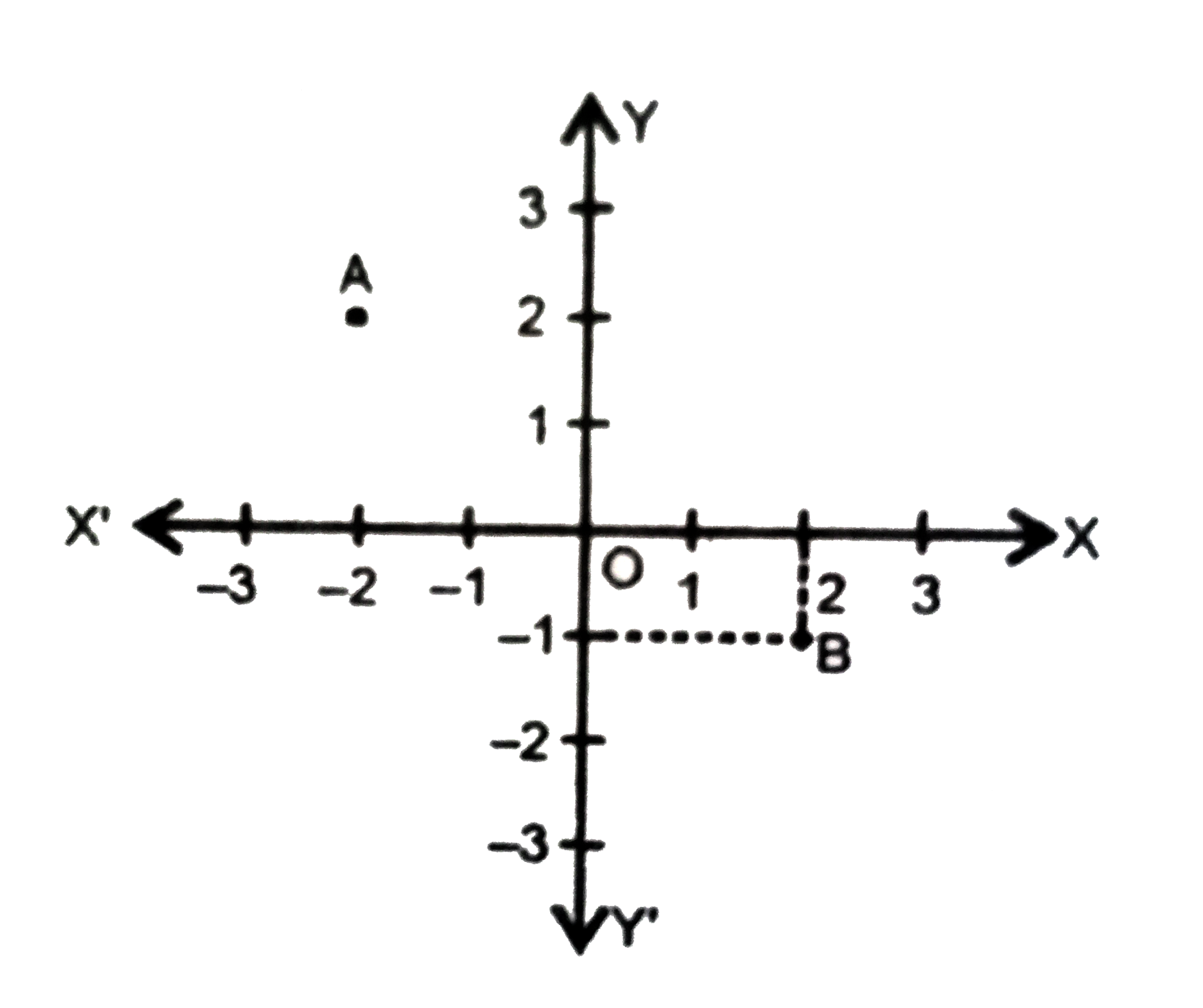 02:02View Solution
02:02View Solution70 विद्यार्थी के प्राप्ताकों का विवरण नीचे तालिका में दिया गया है।
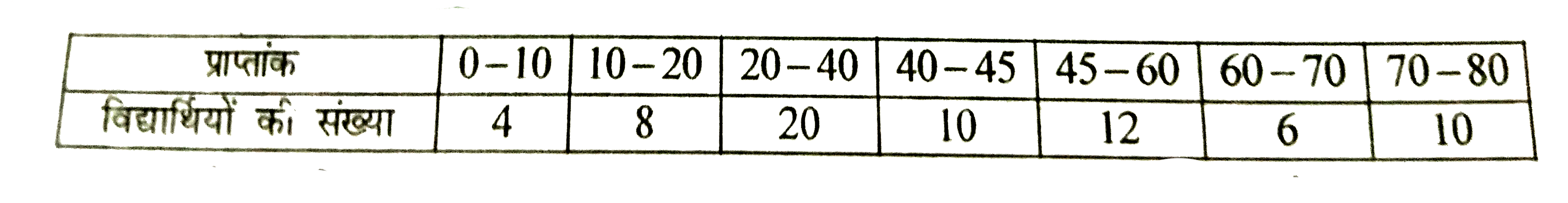
एक विद्यार्थी द्वारा निम्नलिखित वर्ग-अन्तराओं के बीच प्राप्तांकों की प्रायिकता ज्ञात करें।
(i) 0-20 (ii) 0-60View Solution2.0μC कोई बिंदु आवेश किसी किनारे पर 9.0 cm किनारे वाले किसी घनीय गॉउसीय पृष्ठ के केंद्र पर स्थिर है ? पृष्ठ से गुजरने वाला नेट फ्लक्स क्या है ?
02:33View Solutionबिन्दुओं (3,4) और (7,8) को मिलाने वाले रेखाखण्ड को रेखा 2x+3y+7=0 किस अनुपात में विभक्त करती है?
04:25View Solution1सेमी भुजा वाले कितने घनों से 2 सेमी भुजा वाला एक घन बनेगा?
02:50View Solution1 सेमी भुजा वाले कितने घनों से 3 सेमी भुजा वाला एक घन बनेगा?
View Solutionकबीर के अनुसार लकड़ी को काटा जा सकता है, परंतु उसकी अग्नि को उससे अलग नहीं किया जा सकता है क्योंकि
View SolutionA solid cube of volume 13824cm3 is cut into 8 cubes of equal volumes. The ratio of the surface area of the original cube to the sum of the surface areas of three of the smaller cubes is :
13824 घन सेमी आयतन वाले एक ठोस घन को बराबर आयतन वाले आठ घनों में काटा जाता है| आरंभिक घन के पृष्ठ क्षेत्रफल तथा तीन छोटे घनों के पृष्ठ क्षेत्रफलों के योग का अनुपात क्या है ?View SolutionA cube of side 1 m length is cut into small cubes of side 10 cm each. How many such small cubes can be obtained?
1 मी लंबी भुजा वाले किसी घन को 10 सेमी भुजा वाले प्रत्येक छोटे-छोटे घनों में काटा जाता है | ऐसे कितने छोटे घन प्राप्त किये जा सकते हैं ?View SolutionA 9 cm solid metallic cube and a solid metallic cuboid having dimensions 5 cm, 13cm, 31cm are melted and recast into a single cube. What is the total surface area(in cm^2 ) of the new cube? 5 सेमी, 13 सेमी, 31 सेमी आयाम वाले घनाभ और 9 सेमी ठोस धातु घन को पिघलाया जाता है और एक ही घन में पुनर्गठित किया जाता है। नए घन का कुल क्षेत्रफल ( cm^2 में) क्या है?
View Solutionअभिक्रिया को निम्न में से किस रूप में वर्गीकृत किया जा सकता है:
View Solutionना चिपकने वाले भोजन के बर्तन को बनाने के लिए निम्नलिखित में से किसका उपयोग किया जाता है?
View SolutionpH 2 वाले एक जलीय विलयन के निर्माण के लिए, pH 1 वाले HCl के जलीय विलयन के 1 लीटर में कितने लीटर जल को मिलाया जाना चाहिए?
View Solution


