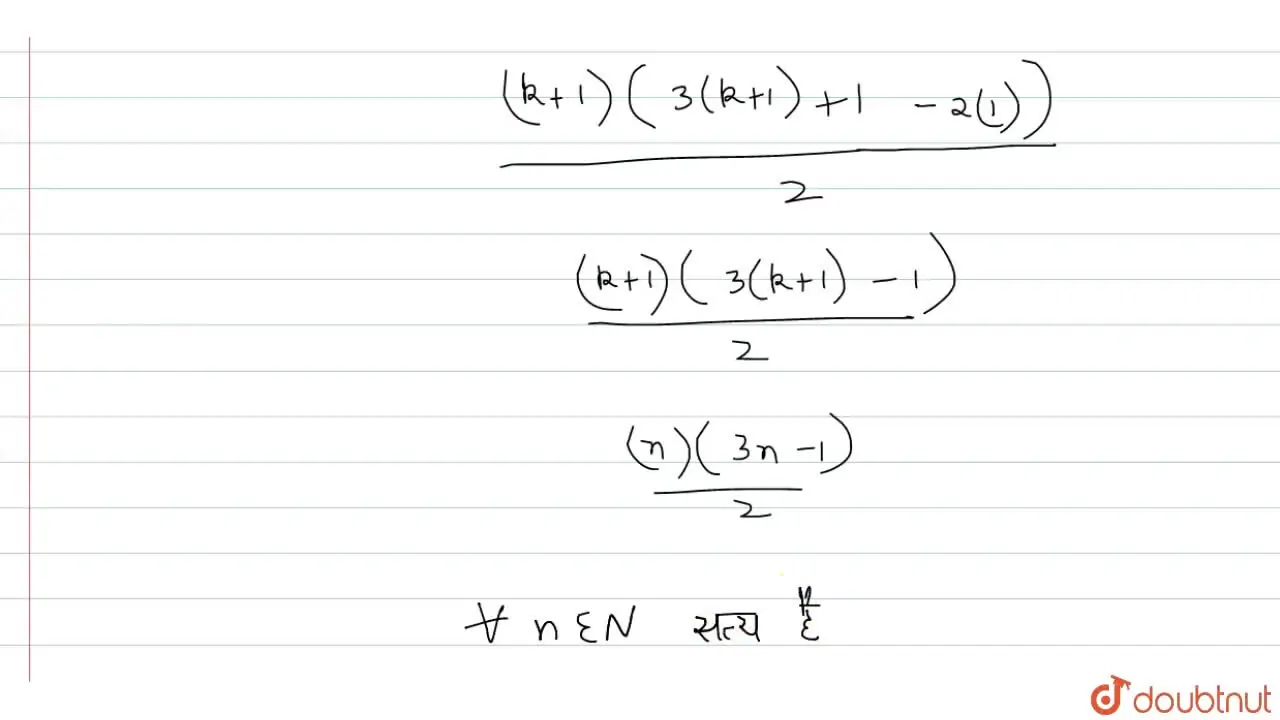आगमन विधि से सिद्ध कीजिए 1+4+7+…+(3n−2)=12n(3n−1) सभी n∈N के लिए।
Step by step video & image solution for आगमन विधि से सिद्ध कीजिए 1+4+7+…+(3n-2)=(1)/(2)n(3n-1) सभी n in N के लिए। by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - RAJEEV BANSALCHAPTER - गणितीय आगमन का सिद्धान EXERCISE - एनसीईआरटी कॉर्नर16videos
गणितीय आगमन का सिद्धान
- BOOK - RAJEEV BANSALCHAPTER - गणितीय आगमन का सिद्धान EXERCISE - कॉम्पिटिशन कॉर्नर8videos
गणितीय आगमन का सिद्धान
- BOOK - RAJEEV BANSALCHAPTER - गणितीय आगमन का सिद्धान EXERCISE - वस्तुनिष्ठ प्रश्न4videos
गणितीय आगमन का सिद्धान
- BOOK - RAJEEV BANSALCHAPTER - गणितीय विवेचन EXERCISE - वस्तुनिष्ठ प्रश्न5videos
गणितीय विवेचन
- BOOK - RAJEEV BANSALCHAPTER - गणितीय विवेचन EXERCISE - वस्तुनिष्ठ प्रश्न (बहुविकल्पीय प्रश्न (एक सही उत्तर)10videos
गणितीय विवेचन
Similar Questions
सभी n∈N के लिए गणितीय आगमन सिद्धांत से निम्नलिखित को सिद्ध कीजिए :
1+3+32+….+3n−1=3n−1203:43View Solutionयदि n∈N हो तब 72n+23n−2.3n−1 हमेशा विभाजित है द्वारा :
02:56View Solutionगणितीय आगमन के सिद्धान के अनुसार 1+2+3+………+n बराबर है :
05:01View Solutionयदि p तथा q कथन है तब समतुल्य कथन को निरुगीत करते है |
03:59View Solutionयदि f(x)=cot(2x+1), तब f'(x) का मान है
01:04View SolutionProve by the principle of mathematical induction that for all n∈N : 1+4+7++(3n−2)=12n(3n−1)
04:41View Solutionlim_(n rarr oo)((4+3n+n^(6))^((1)/(3)))/(1+3n+2n^(2))
04:36View Solution2C_(0)+5C_(1)+8C_(2)++(3n+2)C_(n)=(3n+4)2^(n-1)
06:34View SolutionSimplify (6(8)^(n+1)+16(2)^(3n-2))/(10(2)^(3n+1)-7(8)^(n))
04:38View SolutionFor n∈N,23n+1 is divisisble by __________
View SolutionUsing the principle of mathematical induction, prove each of the following for all n∈N 11⋅4+14⋅7+17⋅10+…+1(3n−2)(3n+1)=n(3n+1).
02:34View Solutionn∈N के लिए, (23n−1) विभाजित होगा:
02:24View Solution12⋅5+15⋅8+18⋅11+............1(3n−1)(3n+2)=n(6n+4)∀n∈N.
04:17View Solution11.4+14.7+17.10+...+1(3n−2)(3n+1)=n(3n+1)∀n∈N.
01:46View SolutionIf n is a positive integer, then value of (3n+2)nC0+(3n−1)nC1+(3n−4)nC2+….+2(nCn) is
06:34View Solution