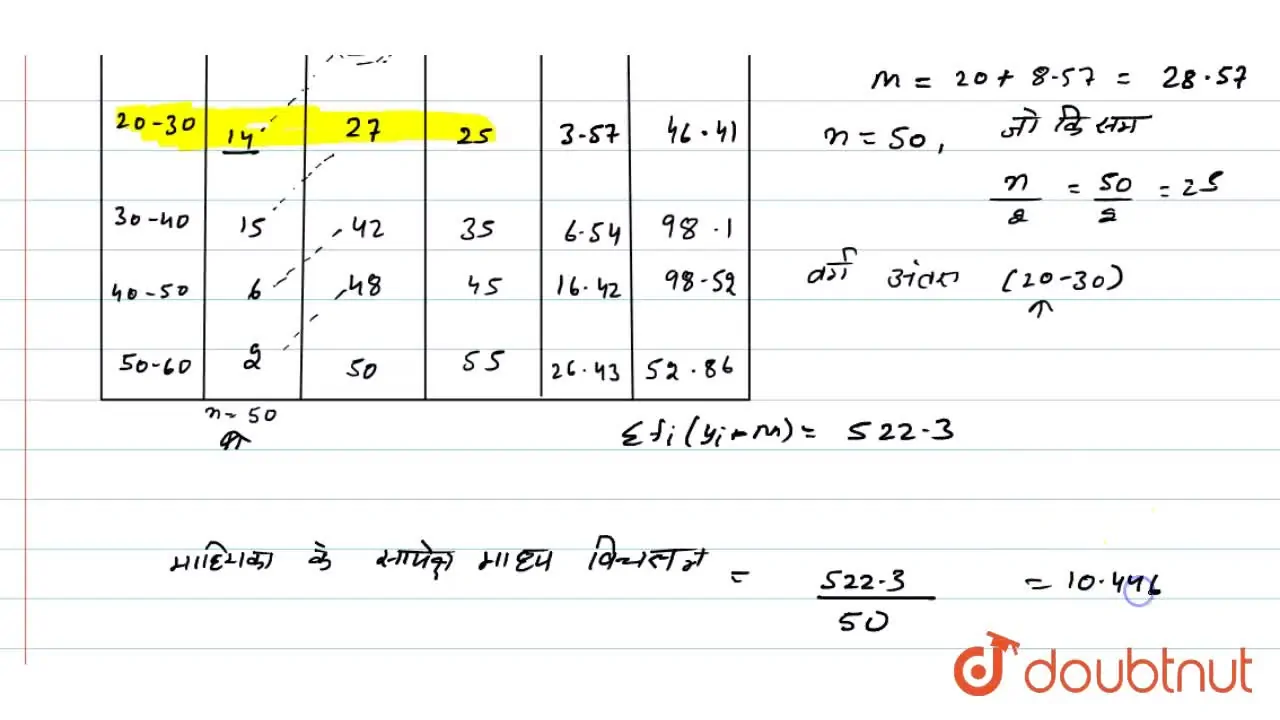
निम्नलिखित आँकड़ो के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए :
वर्ग0−1010−2020−3030−4040−5050−60बारम्बारता 5 8 14 15 6 2

∵N=50 और N2=25 वाँ पद 20 - 30 वाले वर्ग में है ।
∴L=20,c=13,f=14,h=10
माध्यिका (Me)=l+N2−cf×h
=20+25−1314×10
=20+12014=28.57
अतः माध्यिका के सापेक्ष माध्य विचलन , (M.D.)
=1N6∑i=1fi|xi−Me|
=524.2850=10.49.
Related Playlists
- BOOK - MANOHAR RAYCHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 15(A)22videos
सांख्यिकी
- BOOK - MANOHAR RAYCHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 15 (A)3videos
सांख्यिकी
- BOOK - MANOHAR RAYCHAPTER - सरल रेखाएँEXERCISE - प्रश्नावली 10(D)28videos
सरल रेखाएँ
- BOOK - MANOHAR RAYCHAPTER - सीमा और अवकलन EXERCISE - प्रश्नावली 13(C)13videos
सीमा और अवकलन
Similar Questions
निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए :
11, 5, 8, 10, 13, 15, 12, 1, 3, 7, 4, 0, 17, 9, 508:09View Solutionआँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए :
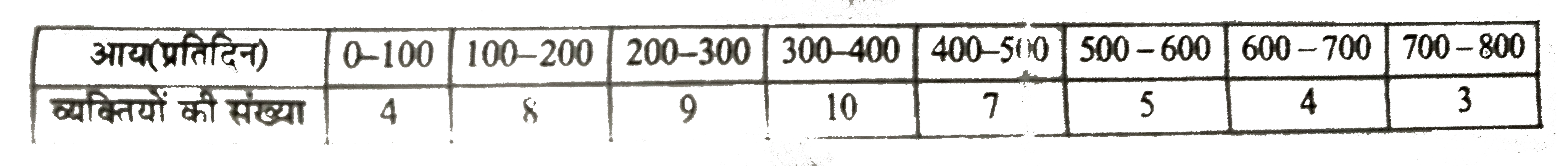 04:58View Solution
04:58View Solution(1 ,2 ) तथा (3 ,7 ) बिन्दुओ से जाने वाली रेखा की ढाल है -
04:35View Solutionनिम्न फलनों के x साक्षेप अवकल - गुणांक प्रथम सिद्धांत से ज्ञात कीजिए :
(i) x3 (ii) −x
(iii) (−x)−1 (iv) √3
(v) 1x2 (vi) x3−27 (vii) (x−1)(x−2) (viii) x+1x−102:53View SolutionObtain the mean , median and mode of the following data : {:("Marks",0-10,10-20,20-30,30-40,40-50,50-60,60-70,70-80),("Number of Students"," "5," "7," "15," "25," "20," "15," "8," "5):}
03:15View Solutionनिम्नलिखित आँकड़ो के लिए लघु विधि द्वारा माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए :
{वर्ग अंतराल0−1010−2020−3030−4040−5050−6060−70बारम्बारता2476145204:27View Solutionनिम्नलिखित बंटन के लिए माध्य , प्रसरण तथा मानक विचलन ज्ञात कीजिए :
वर्ग 0−1010−2020−3030−4040−50बारम्बारता 6 9 12 8 1503:03View Solutionनिम्न बारम्बारता बंटन का समान्तर माध्य ज्ञात करो :
वर्ग अन्तराल: 0−1010−2020−3030−4040−50बारम्बारता: 7 10 15 8 1002:59View Solutionबारम्बारता बंटन का समान्तर मध्य ज्ञात कीजिए
वर्ग अन्तराल : 0−1010−2020−3030−4040−50 बारम्बारता : 9 12 15 10 1405:04View Solutionयदि निम्न बारम्बारता बंटन की मध्यिका 28 .5 हो , तो अज्ञात बारम्बारताओ को ज्ञात कीजिए |
वर्ग अन्तराल :0−1010−2020−3030−4040−5050−60योग बारम्बारता : 5 f1 20 15 f2 5 6004:14View Solutionबारम्बारता बटन का बहुलक ज्ञात कीजिए |
वर्ग अन्तराल :0−1010−2020−3030−4040−5050−6060−7070−80 बारम्बारता : 5 25 39 41 36 17 15 1204:26View Solutionबारम्बारता बटन का बहुलक ज्ञात कीजिए |
वर्ग अन्तराल :25−3030−3535−4040−4545−5050−60 बारम्बारता : 25 34 50 42 38 1402:57View Solutionनिम्न बारम्बारता बंटन का मध्यिका वर्ग लिखिए ।
वर्ग अन्तराल: 0−1010−2020−3030−4040−5050−6060−7070−80बारम्बारताएँ : 5 8 7 12 28 20 10 1003:16View Solutionनिम्नलिखित सारणी से समान्तरमाध्य की गणना कीजिए :
वर्ग0−1010−2020−3030−4040−50बारम्बारता8162514704:25View Solutionनिम्नलिखित सारणी से माध्यिका की गणना कीजिए :
वर्ग0−1010−2020−3030−4040−50बारम्बारता4810121601:58View Solution