With the help of a suitable ray diagram, derive the mirror formula for a concave mirror.
Fig. 9.53(a) and (b), show ray diagram explaining formation of a real image of a linear object AB placed in front of a concave mirror MPN of focal length/. Since aperture of mirror is small, hence MP be considered to be a straight line.

Let us consider right angled triangles A.B.F and MPF, which are similar triangles. Therefore,
B.A.PM/B.FFP
But as PM = AB, hence, we have B.A.BA=B.FFP.......(i)
Again triangles APB and A.PB. are also similar triangles and we have
B.a.BA=B.PBP...........(ii)
compairing (i) and(ii), we getB.PBP=B.FFP=B.P−FPFP
As per sign convention followed :BP =-u, B.P - —v, and FP = -f. Therefore, we get −v−u=(−v)−(−f)−f⇒vu=v−ff
⇒vf=uv−uf or uf+vf=uv
Dividing throughout by uvf, we get
1v+1u=1f, which is the requisite mirror formula.
Related Playlists
- BOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - LONG ANSWER QUESTIONS-II9videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SELF ASSESSMENT TEST (SECTION A)(MULTIPLE CHOICE QUESTIONS)5videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - U-LIKE SERIESCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - SHORT ANSWER QUESTIONS54videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test10videos
NUCLEI
- BOOK - U-LIKE SERIESCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - SECTION B1videos
SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
Similar Questions
(a) Using the necessary ray diagram, derive the mirror formula for a concave mirror.
(b) In the magnified image of a measuring scale (with equidistant markings) lying along the principal axis of a concave mirror, the markings are not equidistant. Explain.View SolutionRay diagram for Concave Mirror
View SolutionWith the help of a ray diagram, determine the position, nature and size of the image formed of an object placed at the centre of curvature of a concave mirror.
View SolutionA mobile phone lies along the principal axis of a concave mirror as shown in Fig. Show by suitable diagram, the formation of its image. Explain why the magnification is not uniform, and distortion will occur depending on the location of the mobile with respect to the mirror.
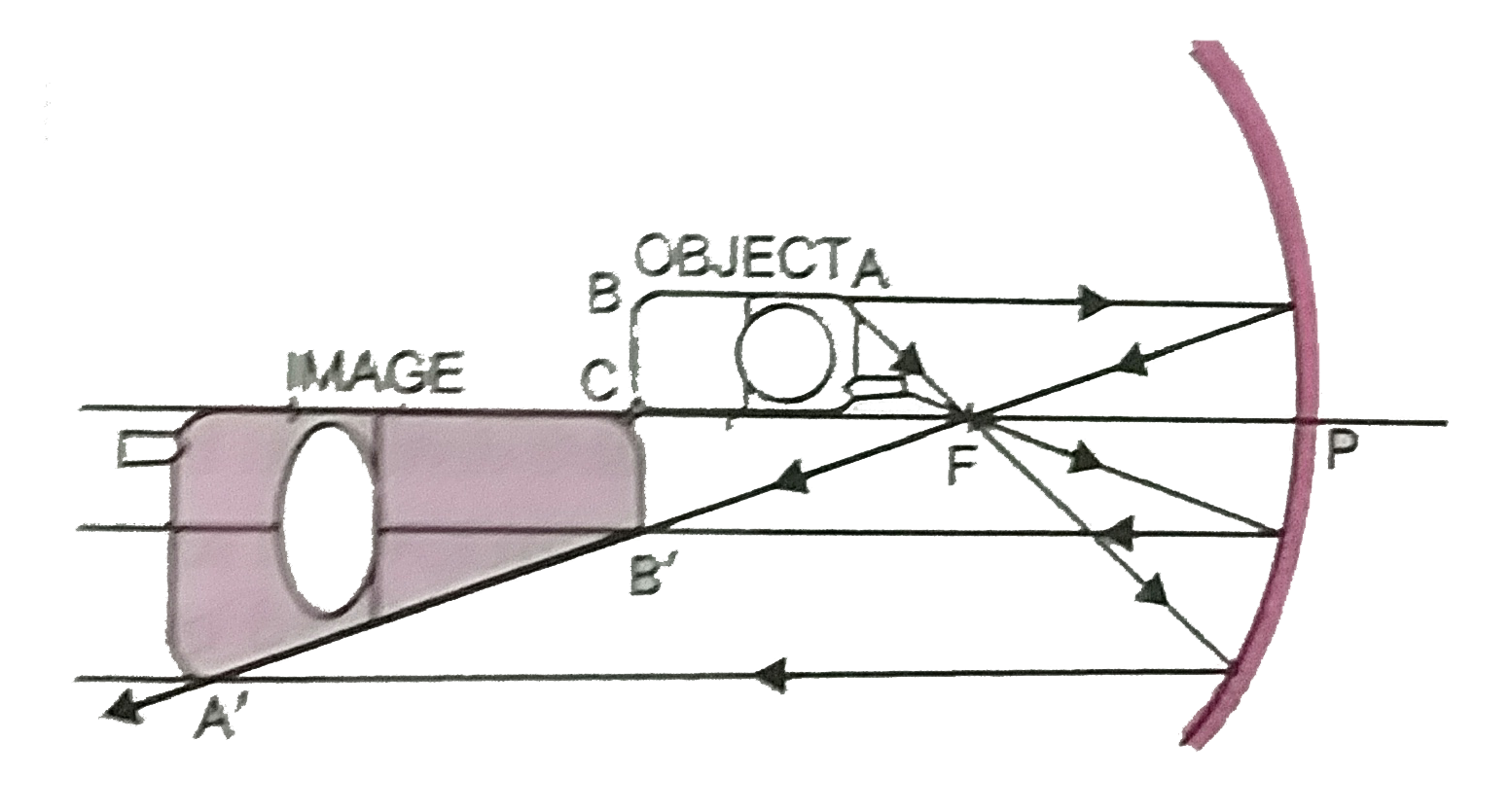 View Solution
View SolutionFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .
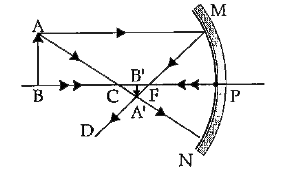
If the focal length of the concave mirror is 10 cm, the image formed will be at a distance ____View SolutionFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .
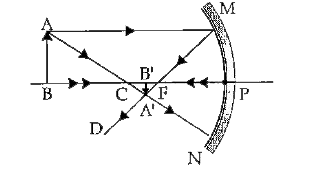
An image formed by concave mirror is virtual, when the object is placed:View SolutionFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .

In case of concave mirror, the image distance is ____ when image is formed in front of the mirror and ____when the image is formed behind the mirror.View SolutionDraw a ray diagram to show the image formation by a concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the image formed.
View SolutionFollowing figure illustrates the ray diagram for the formation of image by a concave mirror. The position of the object is beyond the centre of curvature of the concave mirror. On the basis of given diagram .
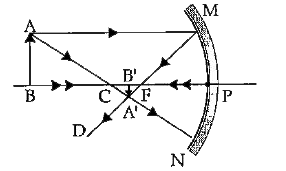
A negative sign in the magnification value indicate that the image is ____View SolutionWith the help of a ray diagram, show the formation of an image of an object placed between principal focus and centre of curvature of a concave mirror.
View Solution

