When the weigth of a body placed on a surface is doubled, how does the coefficient of friction channge ?
To solve the question of how the coefficient of friction changes when the weight of a body placed on a surface is doubled, we can follow these steps:
Step 1: Understand the Definition of Coefficient of Friction
The coefficient of friction (μ) is defined as the ratio of the frictional force (F_friction) to the normal force (N):
μ=FfrictionN
Step 2: Identify the Relationship Between Weight and Normal Force
When a body is placed on a surface, its weight (W) acts downward, and this weight is equal to the normal force (N) exerted by the surface when the body is at rest. Therefore, we can say:
N=W
Step 3: Analyze the Effect of Doubling the Weight
If the weight of the body is doubled, we have:
W′=2W
Thus, the new normal force (N') will also be:
N′=W′=2W
Step 4: Determine the Frictional Force
For the body to remain at rest on the surface, the frictional force must also adjust to balance the increased normal force. If the coefficient of friction remains constant, the frictional force will also double to maintain equilibrium:
F′friction=μ⋅N′=μ⋅(2W)=2Ffriction
Step 5: Conclude About the Coefficient of Friction
Since the coefficient of friction (μ) is defined as the ratio of frictional force to normal force, and both the frictional force and normal force have doubled, the ratio remains the same:
μ′=F′frictionN′=2Ffriction2N=FfrictionN=μ
Thus, the coefficient of friction does not change.
Final Answer
The coefficient of friction remains constant when the weight of the body placed on a surface is doubled.
---
The coefficient of friction (μ) is defined as the ratio of the frictional force (F_friction) to the normal force (N):
μ=FfrictionN
When a body is placed on a surface, its weight (W) acts downward, and this weight is equal to the normal force (N) exerted by the surface when the body is at rest. Therefore, we can say:
N=W
If the weight of the body is doubled, we have:
W′=2W
Thus, the new normal force (N') will also be:
N′=W′=2W
For the body to remain at rest on the surface, the frictional force must also adjust to balance the increased normal force. If the coefficient of friction remains constant, the frictional force will also double to maintain equilibrium:
F′friction=μ⋅N′=μ⋅(2W)=2Ffriction
Since the coefficient of friction (μ) is defined as the ratio of frictional force to normal force, and both the frictional force and normal force have doubled, the ratio remains the same:
μ′=F′frictionN′=2Ffriction2N=FfrictionN=μ
Thus, the coefficient of friction does not change.
The coefficient of friction remains constant when the weight of the body placed on a surface is doubled.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 4Book:ICSEChapter:SELF ASSESSMENT PAPER 4Exercise:Section-B
Explore 13 Videos
- SELF ASSESSMENT PAPER 4Book:ICSEChapter:SELF ASSESSMENT PAPER 4Exercise:Section-C
Explore 9 Videos
- SELF ASSESSMENT PAPER 4Book:ICSEChapter:SELF ASSESSMENT PAPER 4Exercise:Section-D
Explore 6 Videos
- SELF ASSESSMENT PAPER 3Book:ICSEChapter:SELF ASSESSMENT PAPER 3Exercise:Section-D
Explore 6 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-D
Explore 6 Videos
Similar Questions
When normal reaction is halved the coefficient of friction is
View SolutionIn the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5. The minimum weight of the block does not slip on the surface is (x×10)N. The value of x is
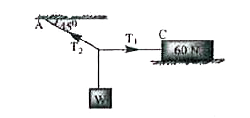
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionA uniform chain is placed at rest on a rough surface of base length l and height h on an irregular surface as shown in figure Then the minimum coefficient of friction between the chain and the surface must be equal to
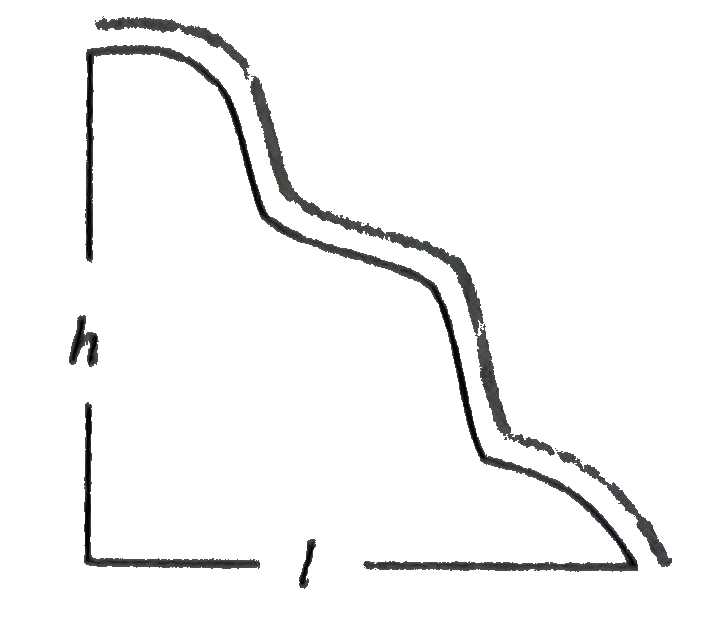
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionIn the given situation disc and ring are connected with a string as shown in the figure. Both are placed on the rough surface of coefficient of friction μ. A force F is applied on the centre of disc horizontally. Then frictional force acting on the ring will be
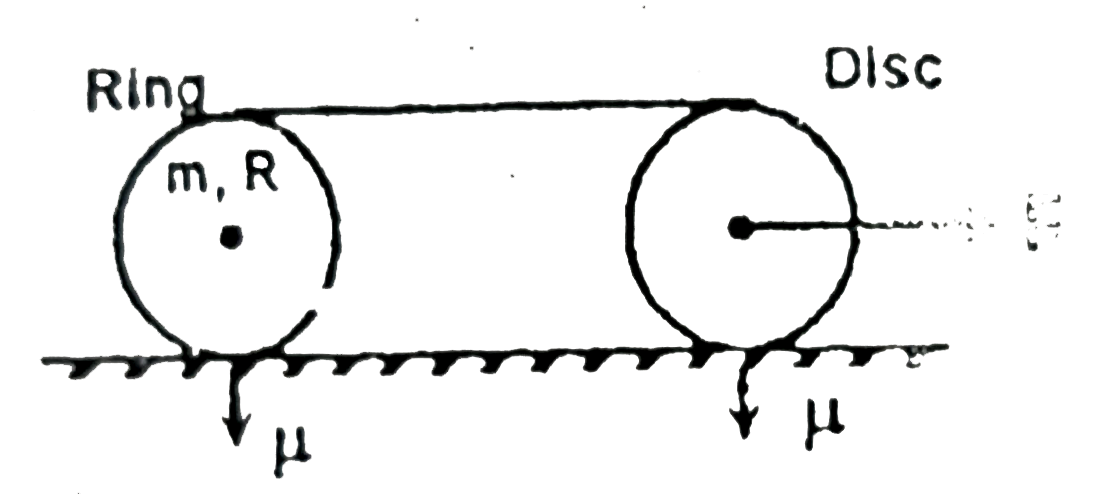
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
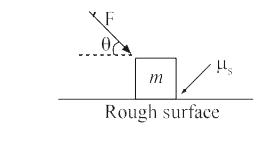
View Solution

