What is the condition for setting up an artificial satellite at a height h from the earth's surface ? (Radius of the earth=R , mass of the earth =M)
Suppose height of the artificial satellite from the earth.s surface is h .
Hence, the radius of the orbit is (R+h) . If v is the orbital speed, the centripetal force necessary to keep the satellite in that orbit is mv2(R+h) ( m= mass of the stellite ). if the mutual force of gravitation between the earth and the satellite can supply this centripetal force, the satellite would be in the orbit. Gravitational force between the satellite and the earth is GMm(R+h)2.
Hence, the necessary condition is
mv2R+h=GMm(R+h)2or,v=√GMR+h
Topper's Solved these Questions
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBook:CHHAYA PUBLICATIONChapter:NEWTONIAN GRAVITATION AND PLANETARY MOTIONExercise:EXERCISE (Multiple choice Questions)
Explore 55 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBook:CHHAYA PUBLICATIONChapter:NEWTONIAN GRAVITATION AND PLANETARY MOTIONExercise:EXERCISE (Very Short Answer Type Questions)
Explore 67 Videos
- NEWTONIAN GRAVITATION AND PLANETARY MOTIONBook:CHHAYA PUBLICATIONChapter:NEWTONIAN GRAVITATION AND PLANETARY MOTIONExercise:SECTION RELATED QUESTIONS
Explore 18 Videos
- NEWTON'S LAWS OF MOTIONBook:CHHAYA PUBLICATIONChapter:NEWTON'S LAWS OF MOTIONExercise:CBSE SCANNER
Explore 24 Videos
- ONE - DIMENSIONAL MOTION Book:CHHAYA PUBLICATIONChapter:ONE - DIMENSIONAL MOTION Exercise:CBSE SCANNER
Explore 19 Videos
Similar Questions
An astronaut of mass m is working on a satellite orbiting the earth at a distance h from the earth's surface the radius of the earth is R while its mass is M the gravitational pull FG on the astronaut is
View SolutionGravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
View Solution
Knowledge Check
A geostationary satellite is at a height h above the surface of earth. If earth radius is R-
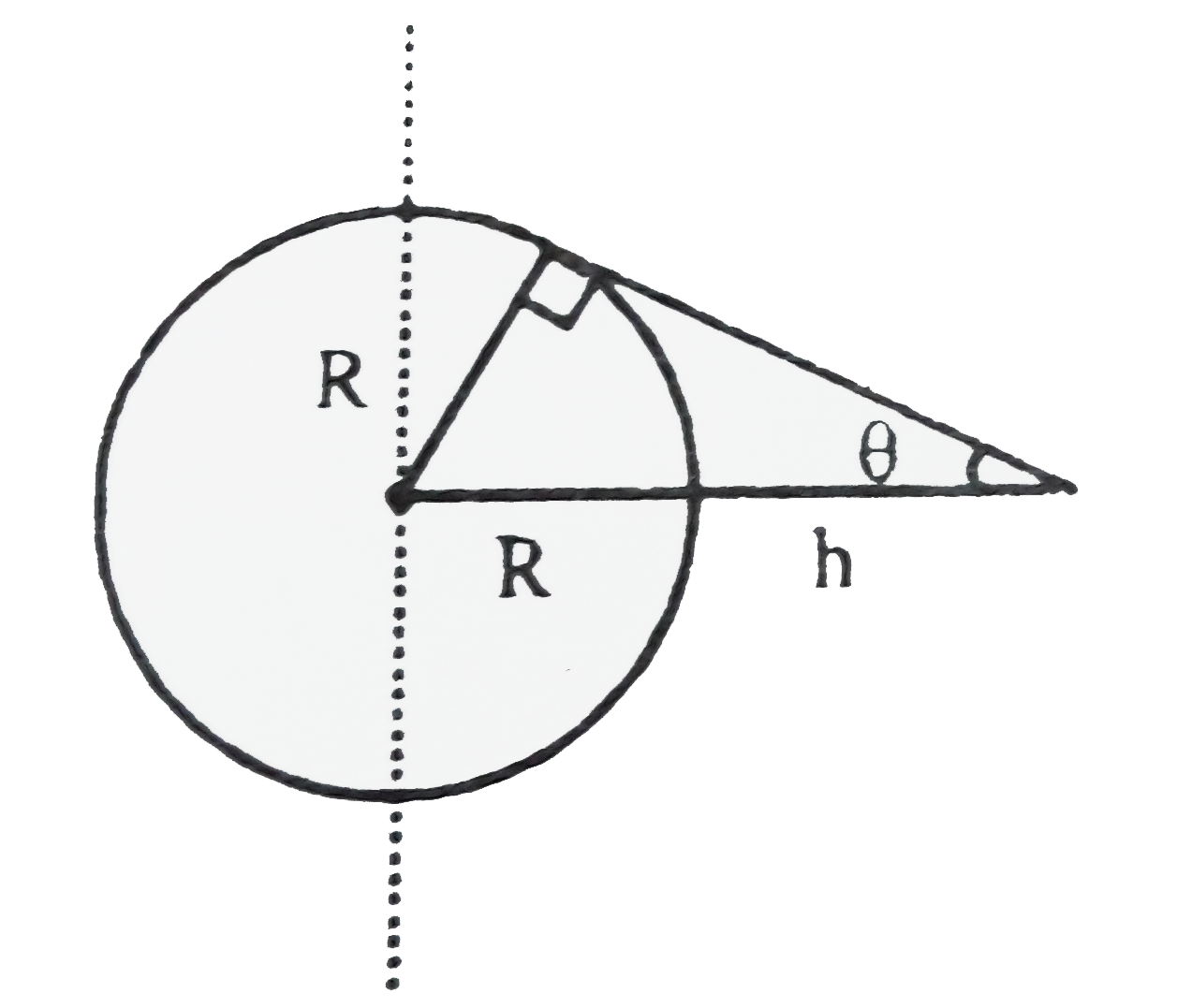 AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)An astronaut of mass m is working on a satellite orbitting the earth at a distance h from the earth's surface the radius fo the earth is R while its mass is M the gravitational pull FG on the astronaut is
Azero since astronaut feels weightlessB0<FG<GMmR2CGMm(R+h)2<FG<GMmR2DF0=GMm(R+h)2Gravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
A−GM2RB−GMRC−GM4RD−GM
At what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 2R from the surface of the earth (R=radius of earth)
View SolutionAt a height H from the surface of earth, the total energy of a satellite is equal to the potential energy of a body of equal mass at a height 3R from the surface of the earth (R = radius of the earth). The value of H is
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 2R from the surface of the earth (R=radius of earth)
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 3R from the surface of the earth (R=radius of earth)
View SolutionAt a height H from the surface of earth, the total energy of a satellite is equal to the potential energy of a body of equal mass at a height 3R from the surface of the earth (R = radius of the earth). The value of H is
View Solution

