Using Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
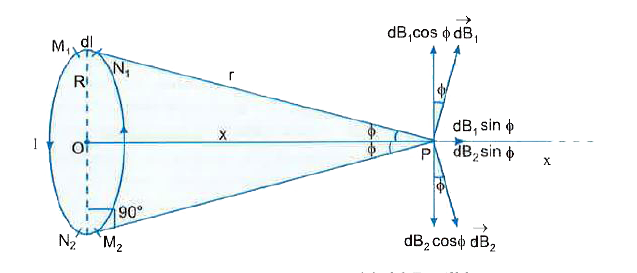
Consider a circular loop of radius R, carrying a current I. Plane of the coil is Y-Z plane (i.e., perpendicular to the plane of paper), while the axis of the loop OX lies in the plane of paper. Consider the circular loop to be divided into large number of current elements I→dt. Two such elements N1M1andN2M2, diametrically opposite to each other, produce the magnetic fields −−→dB1and−−→dB2 perpendicular to both →rand→dl and given by right hand rule as,
∣∣∣−−→dB1∣∣∣=∣∣∣−−→dB2∣∣∣=μ04π.Idlsin90∘r2=μ04πIdl(R2+x2)
These fields may be resolved into components along x -- axis and y - axis. Obviously components along y - axis balance each other but components along x - axis are all summed up. Hence, magnetic field due to whole current loop will be :
B=∮dBsinϕ=∮μ0(R2+x2).R√(R2+x2)=μ0IR4π(P2+x2)3/2∮dl
=μ0IR4π(R2+x2)3/2.2πR=μ0IR22(R2+x2)3/2
For a point at the centre of circular coil x = 0, so value of field B will be
B=μ0IR22R3=μ0I2R
Related Playlists
- BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION D6videos
CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)
- BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION B9videos
CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)
- BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - D6videos
CBSE EXAMINATION PAPER 2020 (SOLVED)
- BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION C )3videos
CURRENT ELECTRICITY
Similar Questions
State the Biot-Savart law. Use it to obtain an expression for magnetic field at the centre of a current carrying circular loop.
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to circular wire carrying current I.View SolutionUse Biot-Savart law to derive the expression for the magnetic field on the axis of a current carrying circular loop of radius R.
Draw the magnetic field lines due to circular wire carrying current I.View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionState Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View Solution

