Two rings having masses and respectively, having the same radius are placed coaxially as shown in the figure.
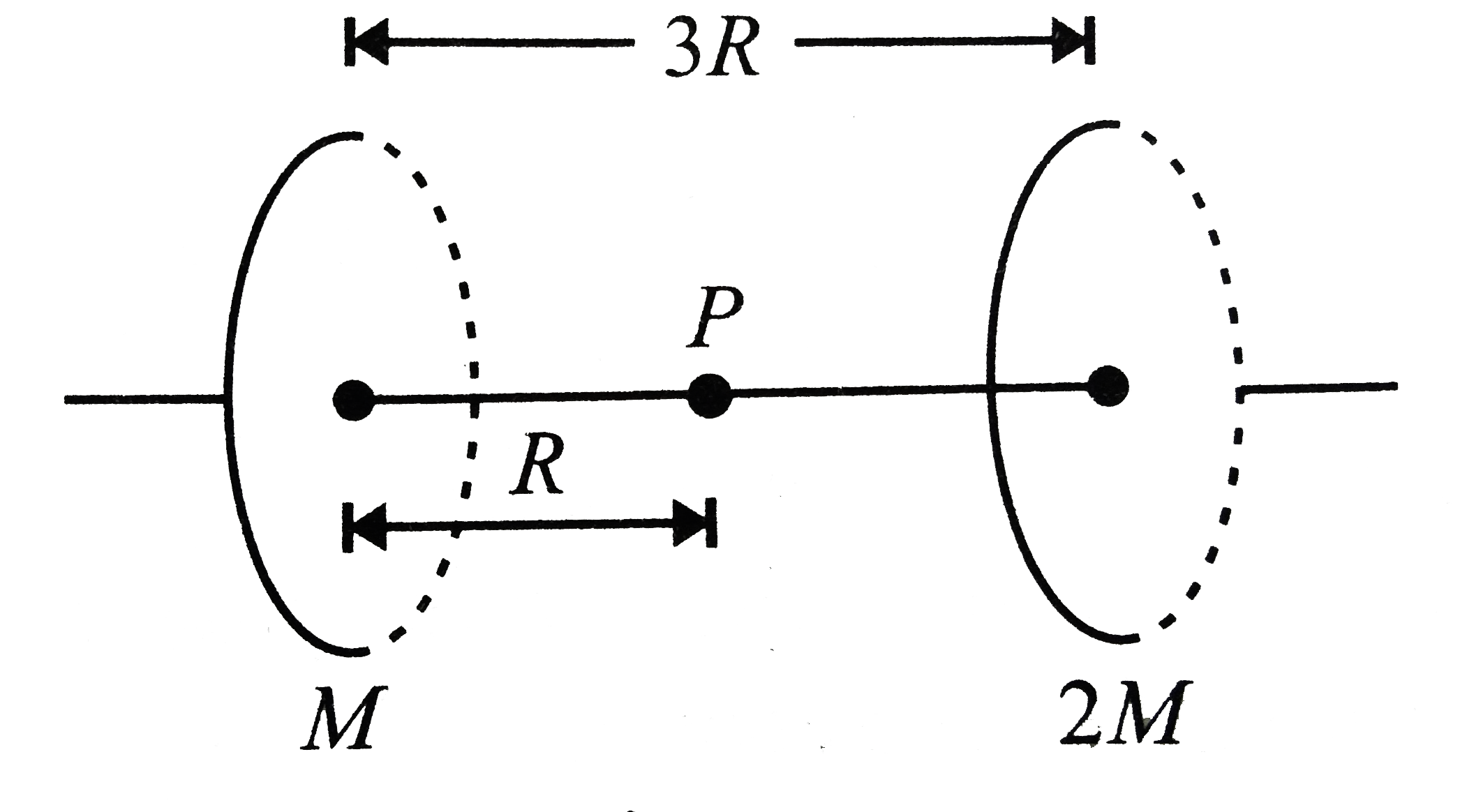 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point is
(a)
(b)
(c)zero
(d)cannot be determined from the given information
The correct Answer is:A
As all the points on the periphery of eigher ring are the same distance from point , the potential at point due to the whole ring can be calculated as where is the axis distance from the centre of the ring. This expression is independent of the fact whether the distribution of mass is uniform or non uniform.
So at
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
Knowledge Check
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMR
Figure show a hemispherical shell having uniform mass density The direction of gravitational field at point P will be along
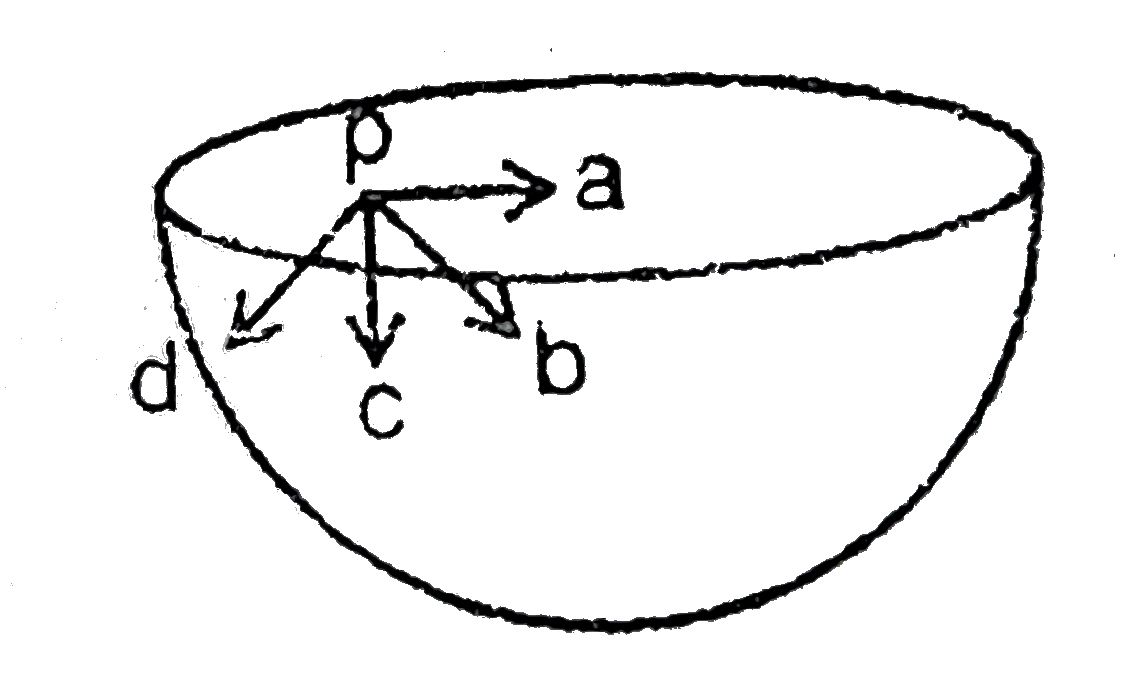 .
.
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionThree rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
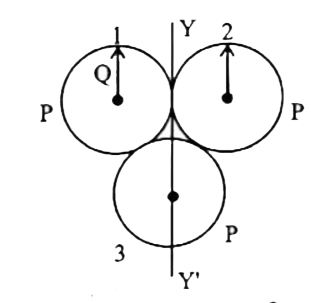
View SolutionTwo rings having same moment of inertia have their radii in the ratio 1 : 4. Their masses will be in the ratio
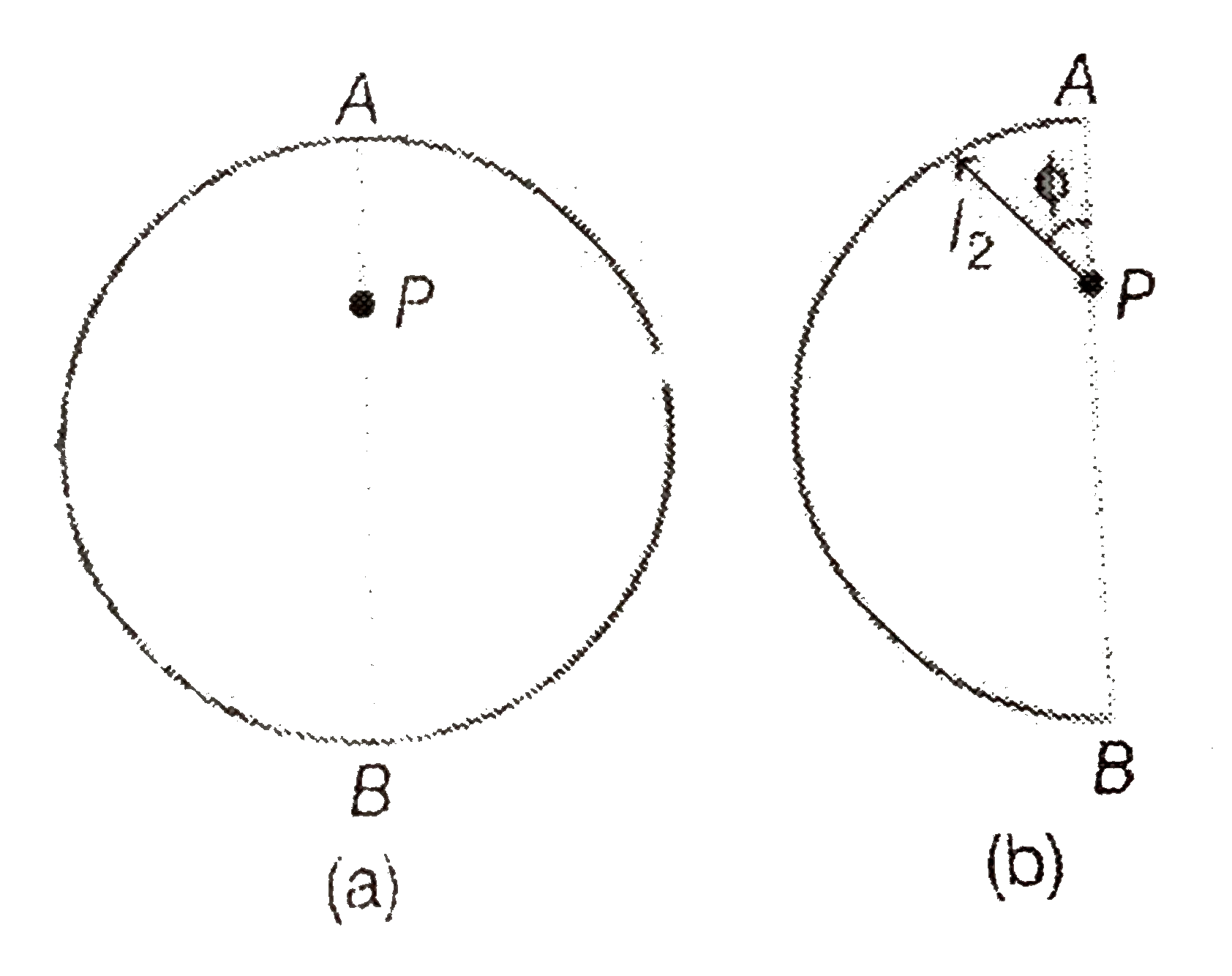
View SolutionFigure (a) shows a ring of mass m and figure (b) shows half portion of the same ring . Gravitational field at point P in figure (b) is I2 in magnitude and makes an angle ϕ with line . AB. Gravitational field at point P in figure (a) is I1 in magnitude . The ratio of I12I2 is
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
View Solution



