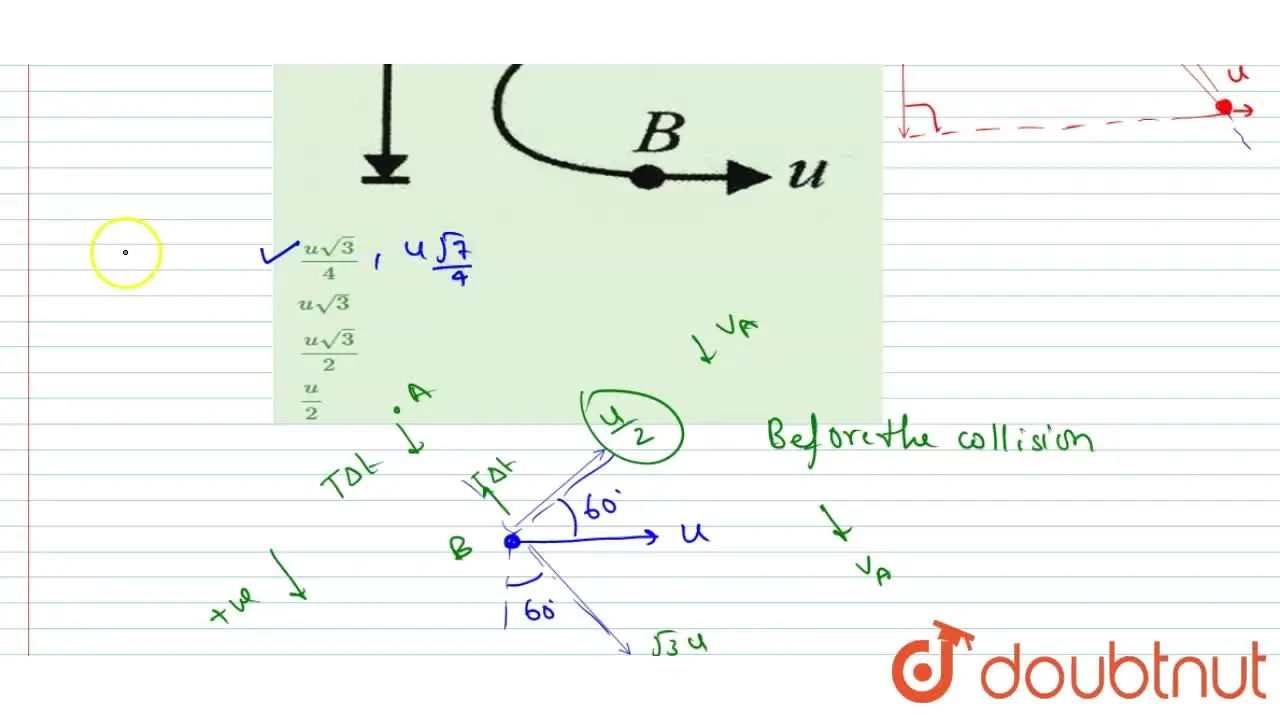
Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
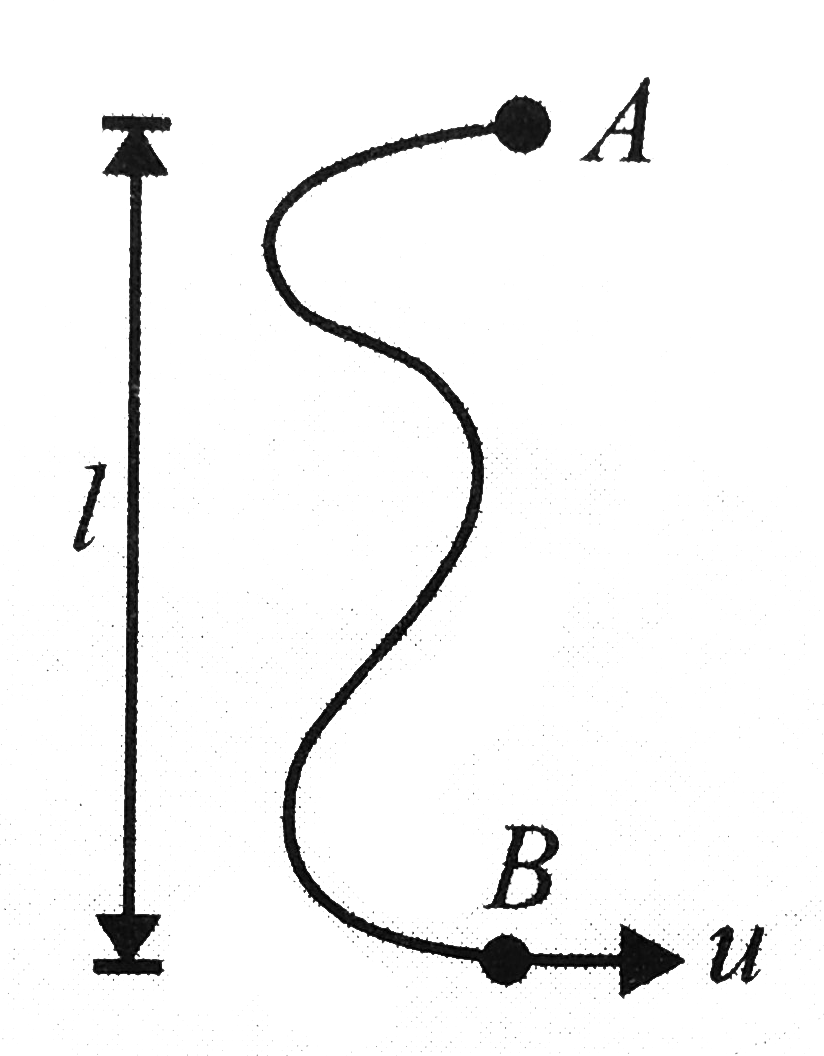
u√34
u√3
u√32
u2
Step by step video & image solution for Two particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct1videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
Similar Questions
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be
 View Solution
View SolutionA particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate
a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.
 View Solution
View SolutionTwo paricles A and B of equal masses m are t ied with an inextensible string of length 2l. The initial distance between A and B is l. Particle A is given speed v as shown. Find the speed of particie A and B just after the string becomes taut.
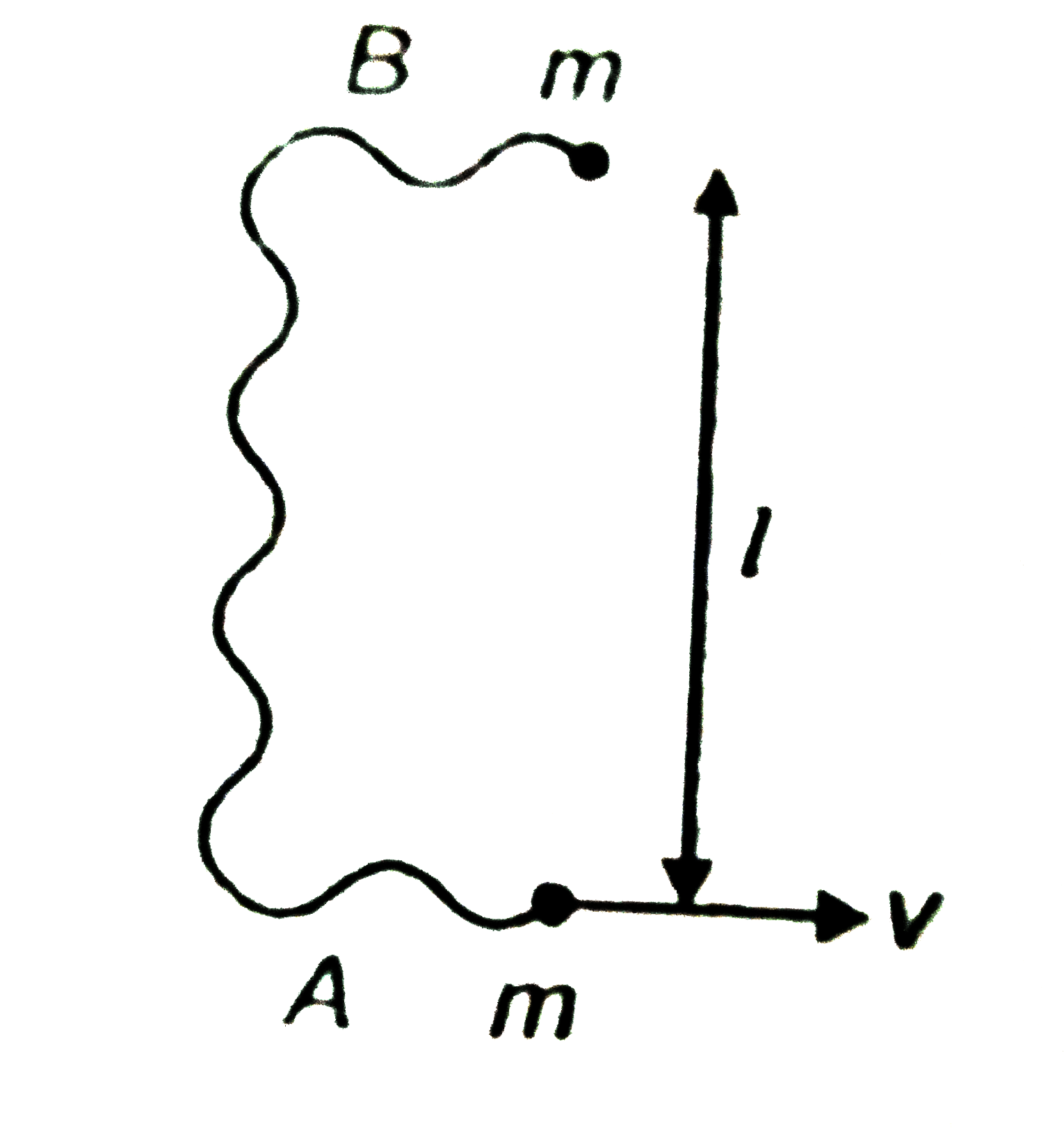 View Solution
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View SolutionTwo masses A and B connected with an inextensible string of length l lie on a smooth horizontal plane. A is given a velocity of vm/s along the ground perpendicular to line AB as shown in figure. Find the tension in string during their subsequent motion
 View Solution
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
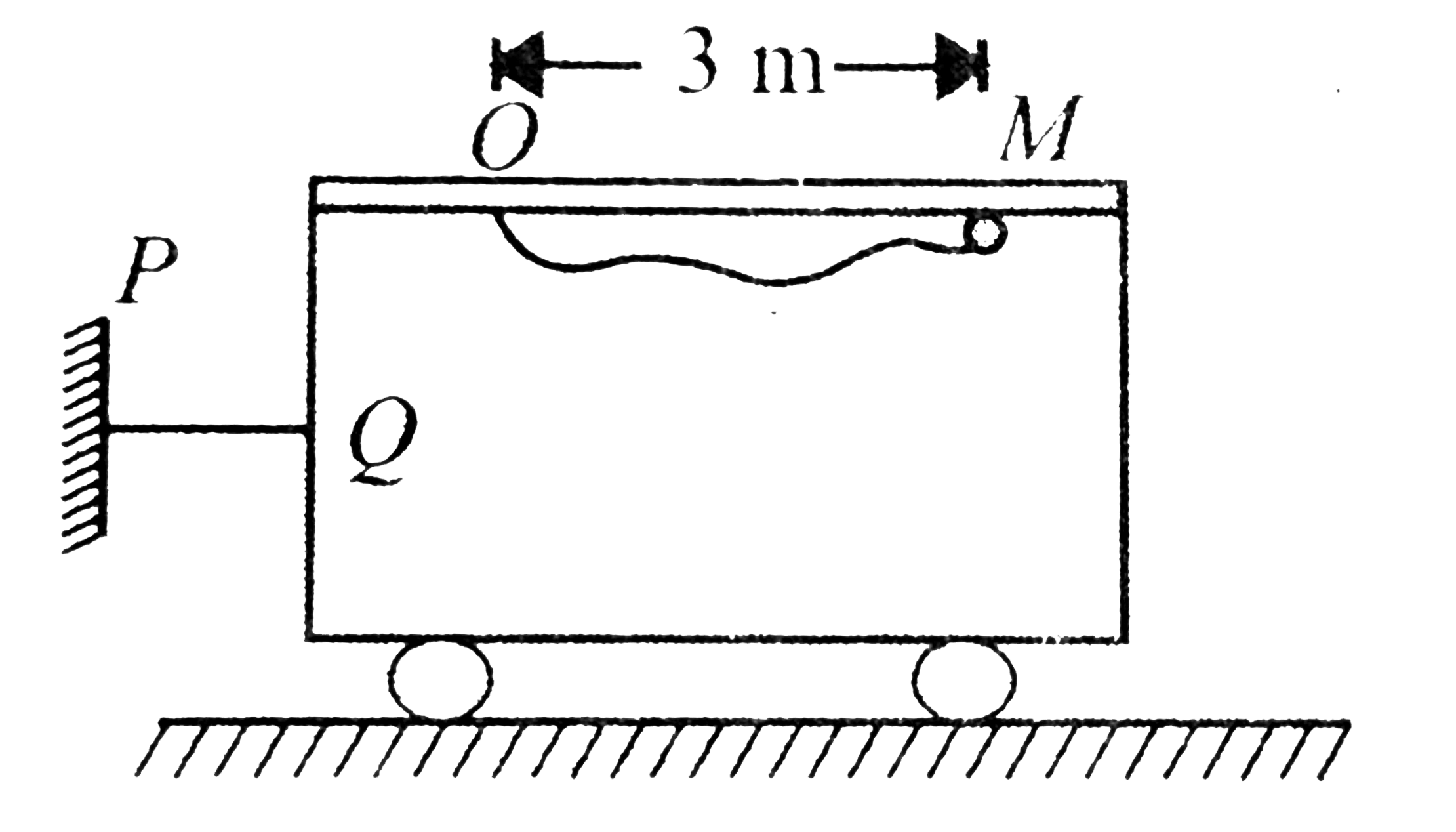
Find the velocity of the particle with respect to C before the collisionView SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then
 View Solution
View Solution