Two identical rods each of mass m and length are connected as shown. Locate c.m.
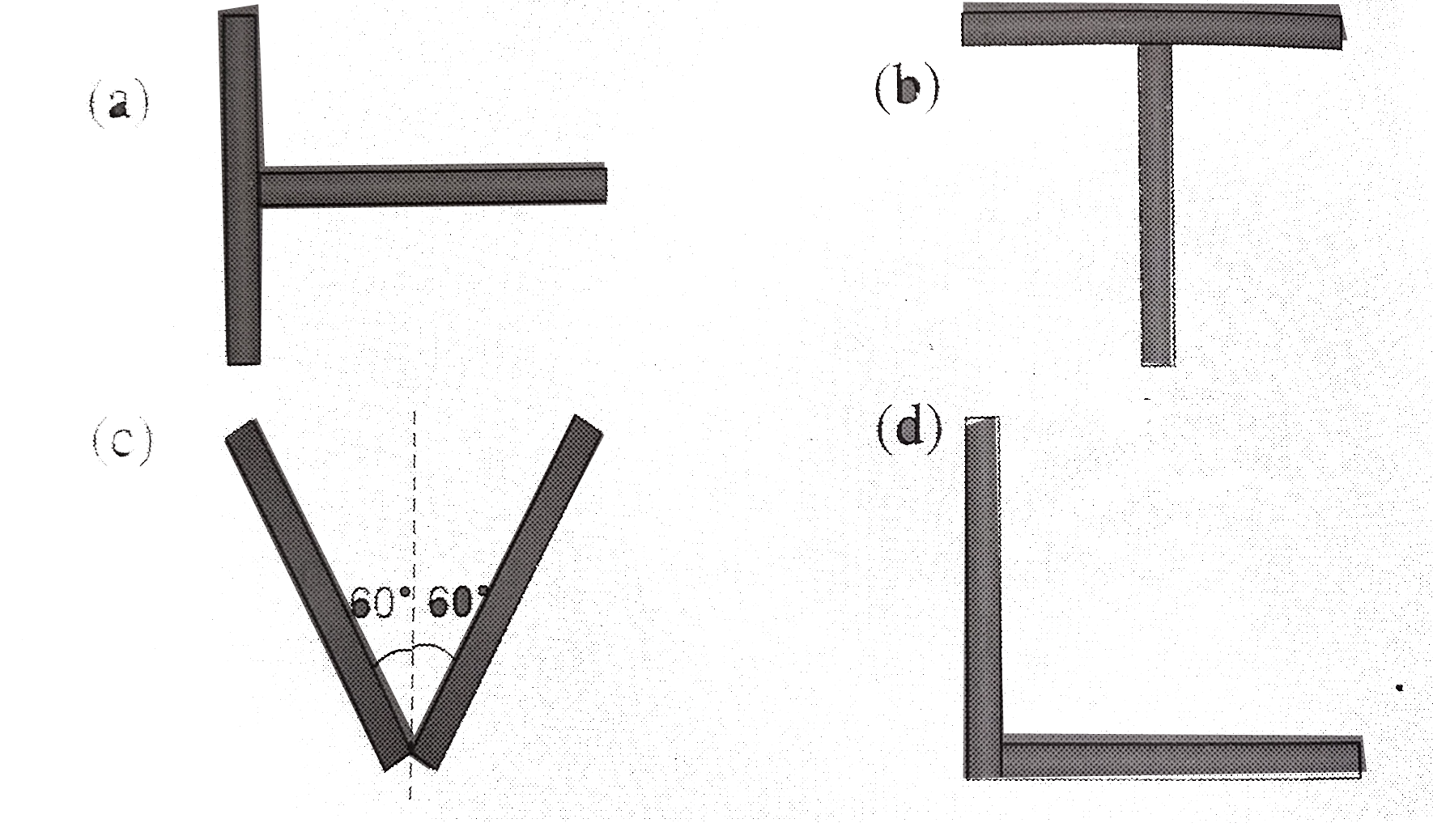
This system is symmetrical about the x-axis. Hence, we need to find xcm. Here we will take coordinate of CM of rods.
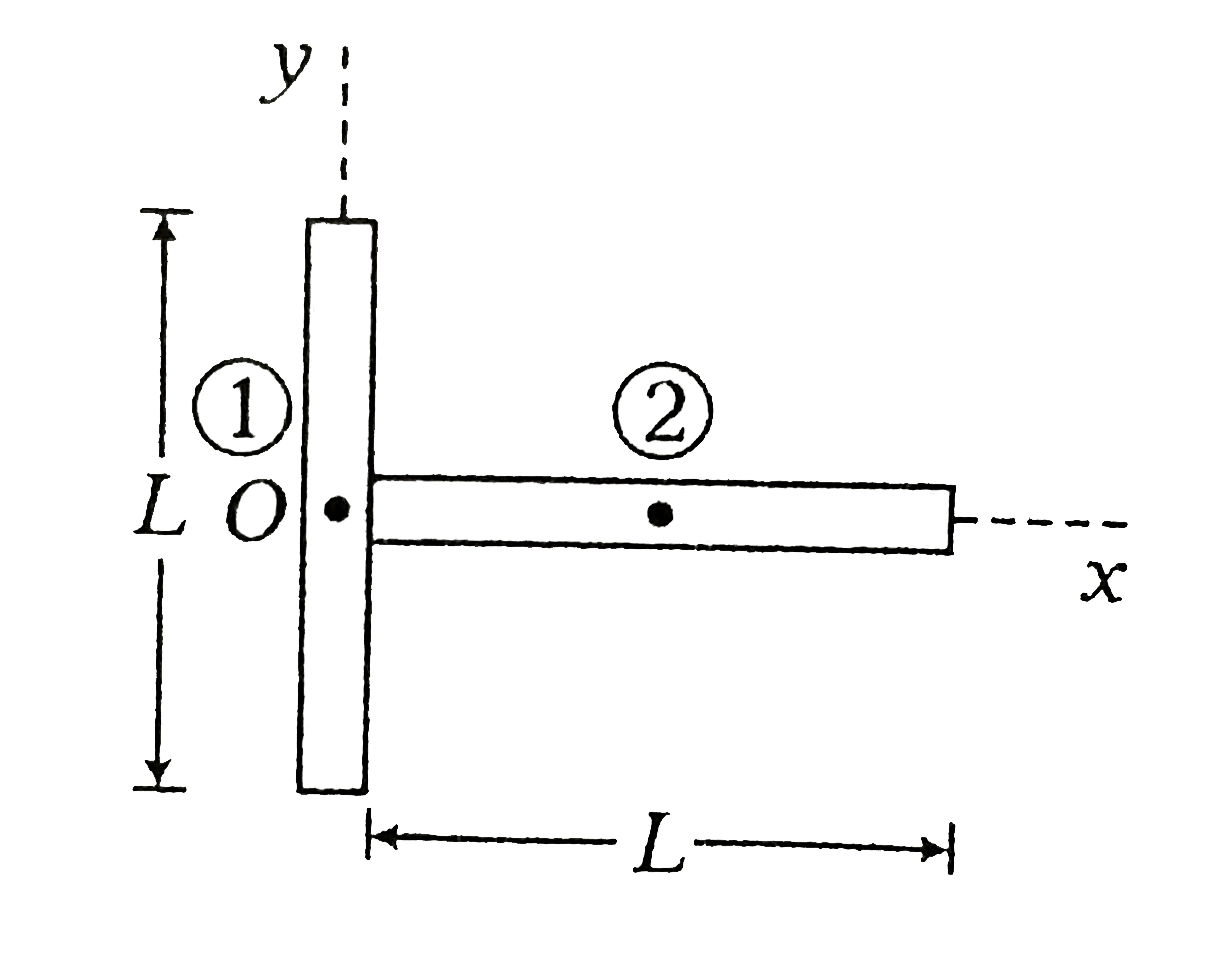
For rod 1, mass m_(1) = m
x-coordinate x1=0
For rod 2, mass m2 = m
x-coordinate x2=L2
∴xCM=m1x1+m2x2m1+m2
xCM=m×0+m×L2m+m=mL22m=L4
Similarly, yCM = 0
∴ Center of mass ≡(L4,0)
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points50videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
Two identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 View Solution
View SolutionTwo uniform rods each of mass M and length L are joined as shown in the figure. The moment of inertia of the system about line AB is kML2.Find the value of k.
View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure
 View Solution
View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View SolutionTwo uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle θ,find the period of oscillations:
 View Solution
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is
 View Solution
View SolutionTwo identical ladders, each of mass M and length L are resting on the rough horizontal surface as shown in the figure. A block of mass m hangs from P. if the system is in equilibrium, find the magnitude and the direction of frictional force at A and B.
 View Solution
View SolutionThree uniform rods, each of mass M and length l, are connected to form an equilateral triangle in a gravity free space. Another small body of mass m is kept at the centroid. Find the minimum velocity v to be given to mass m so that it escapes the gravitational pull of the triangle.
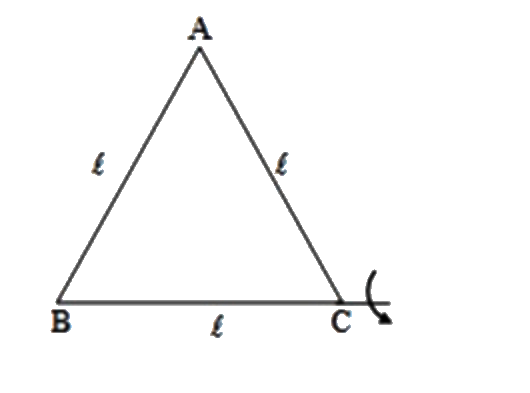
View SolutionThree identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
 View Solution
View Solution


