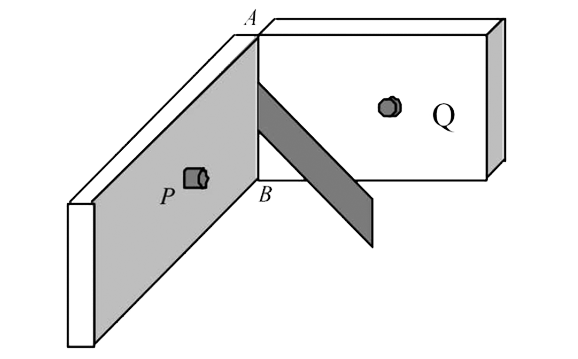
Two heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacal is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
(i) 0.1, (ii) 1
Let x be the distance of centre of the mass from AB.
Moment of inertia of the laminar sheet about an axis passing through centre of mass and paralel to AB=1.2kgm2

IAB=ICM+MX2.........(i)
Impulse =MV2+(−v1)=M(v2+v1)
Where ω1, and ω2 are the angular velocities of the sheet before and after the collision with obstacles.
Impulsive torque =−6×0.5=Lt−L1
Li=Lt+3⇒(Li−Lf)=3
IAB(ω1−ω2)=3⇒IAB(ω1+ω2)=3........(iii)
From equations (ii) and (iii), IAB=Mx2
IAB=Mx2=1.2+Mx2⇒30x2−15x+1.2=0,x=15±960=0.4 o 0.1m
(i) Substituting x=0.4m in equation (ii)
6=30(0.4)(ω2+1)⇒ω2=−0.5 (this is not possible)
The laminar sheet turns back after collision.
(ii) Substituiting x=0.1 m in equation (ii)
6=30(0.1)(ω1+1)
Angular velocity of lamination sheet after collision =1 rad/s.
Ths is possible if collision is elastic.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (FILL IN THE BLANKS TYPE)14videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (True/False Type)3videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MATRIX MATCH TYPE)1videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionConsider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
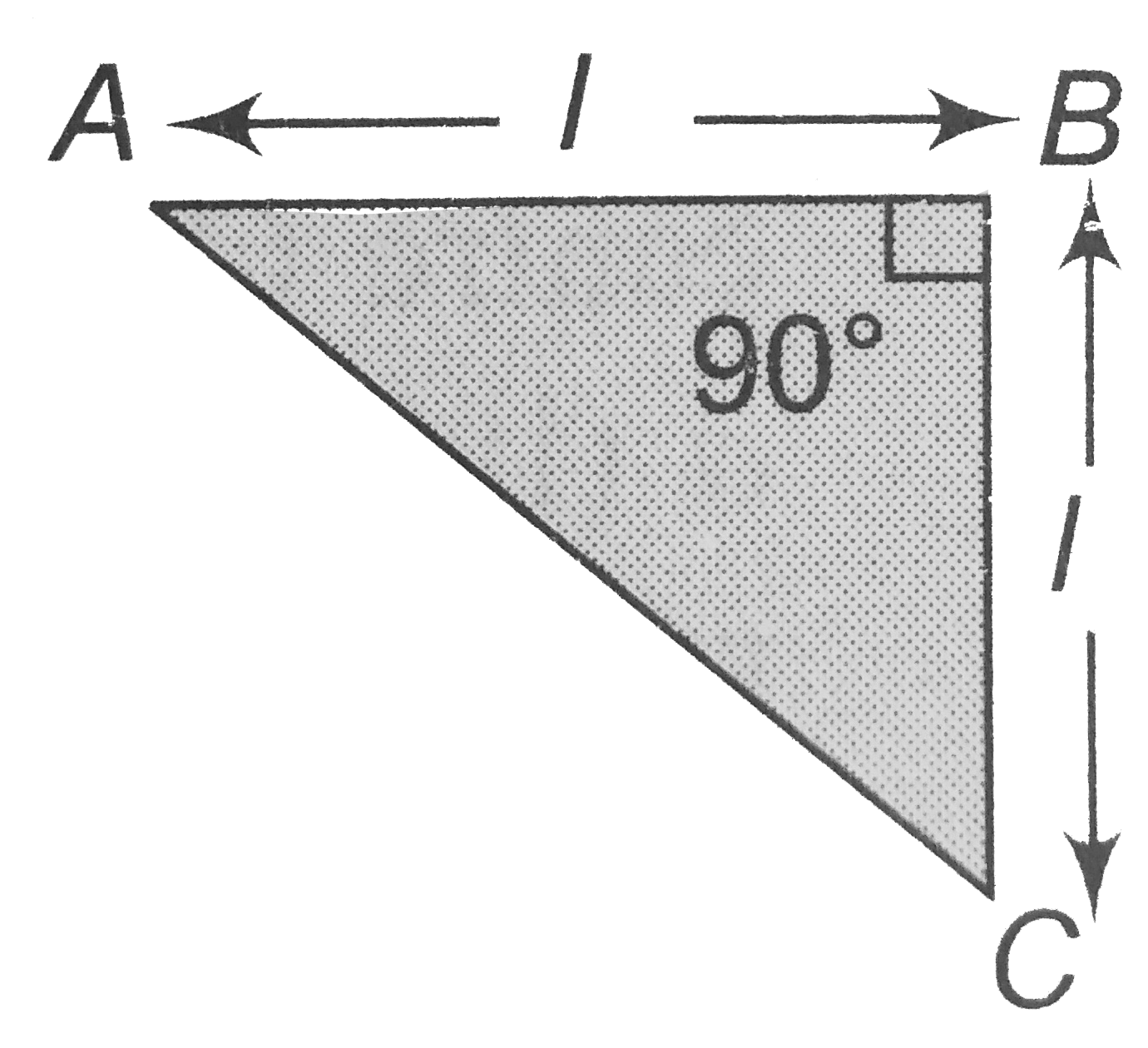
View SolutionFigure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
 .View Solution
.View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?
 View Solution
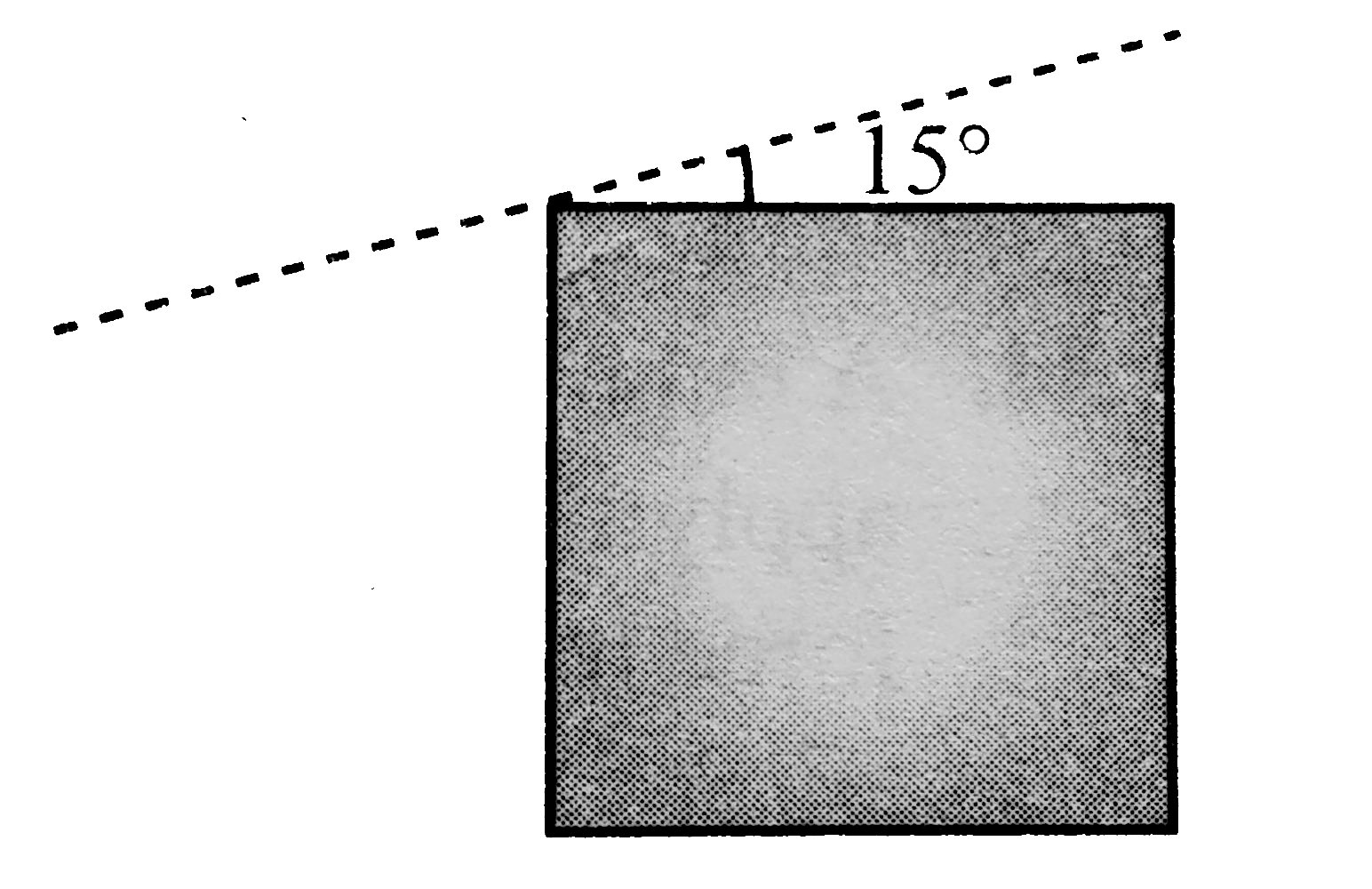
View SolutionA square plate of mass M and edge L is shown in the figure. The moment of inertia of the plate about the axis in the plane of plate and passing through one of its vertex making an angle 15∘ horizontal is
 View Solution
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View Solution


