Two cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)
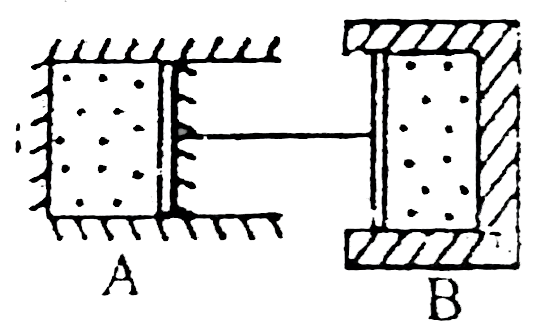
What will be the compressive force in conneting rod at equilibrium
PS
√2 PS
23/2PS
none
The correct Answer is:C
P0V0=mMRT ina cylinder....(1)
PBV0=mBMRT in Bcylinder.....(2) adiabatic
P0Vγ0=Pf(V02)γ
Pf=2√2P0=PB
Divide((1))//(2) P0V0PBVB=mmBVB=32V0
P0V02√2P0(32V0)=mmB
mB=3√2m
ΔU=−W=(PfVf−PiViγ−1)=2P0V02×2√2−P0V0(3/2)−1=2(√2−1)P0V0
Fcompressive=PfArea=2√2Ps
WA=(PiVi−PfVfγ−1)=P0V0−2√2P0(V0/2)(3/2)−1=2P0V0(1−√2)
|WA|=0.828P0V0=P0V0(2(1−11.414)=P0V0(−0.828)=−0.828P0V0
T=C=nRT0ln(VfVi)=PfVfln(3V02V0)=2√2P0(3V02)ln(32)=3√2P0V0ln(32)
=[3√2ln(1.5)P0V0]=(4.242×0.40)P0V0
WB=1.719P0V0
|WB|=1.719P0V0
|WA|<|WB|
Related Playlists
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective131videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Statement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.02:55View SolutionThe quantity// quantities that does //do not have mass in its// their dimentions (when we take standard 7 quantities as fundmental) is//are:
07:25View SolutionThe manifestation of band structure in solids is due to
07:25View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
07:25View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
04:57View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) The mass of gas in cylinder B
04:29View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)

The change in internal energy of gas in cylinder AView SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA then01:36View SolutionTwo cylinder A and B fitted with pistons contain equal number of moles of an ideal monoatomic gas at 400 K . The piston of A is free to move while that of B is held fixed . Same amount of heat energy is given to the gas in each cylinder . If the rise in temperature of the gas in A is 42 K, the rise in temperature of the gas in B is
04:57View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300 K. The piston of A is free to move, while that of B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30 K, then the rise in temperature of the gas in B is :
04:57View SolutionA cylinder with two ends is equipped with a moving piston. The gas on one side of the piston has a mass M and the other side has a mass of 2m of the same gas. If the piston is in equilibrium state, how much volume of the cylinder will be surrounded by the greater mass of gas while the temperature is the same in the whole cylinder?
03:47View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300 K. The piston of A is free to move, while that of B is held fixed. The same amount of heat is given to the gas ineach cylinder. If the rise in temperature of the gas in A to 30 K, then the rise in temperature of the gas in B is
02:11View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move while that of B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30 K, then the rise in temperature of the gas in B is :
03:39View SolutionTwo cylinder A and B fitted with pistons contain equal number of moles of an ideal monoatomic gas at 400 K . The piston of A is free to move while that of B is held fixed . Same amount of heat energy is given to the gas in each cylinder . If the rise in temperature of the gas in A is 42 K, the rise in temperature of the gas in B is
02:33View Solution


