Two coherent point sources vibrating in phase light of wavelength . The separation between the sources is . The smallest distance from on a line passing through and perpendicular to where a minimum of intensity occurs is
Path difference at . Therefore for minimum intensity at P let x be the minimum distance from . Then
or
Solving this equation we get
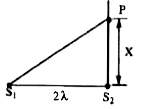 .
.
Topper's Solved these Questions
Similar Questions
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .View Solution
.View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .A7λ12B15λ4Cλ2D3λ4
.A7λ12B15λ4Cλ2D3λ4 - Question 2 - Select One
Choose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
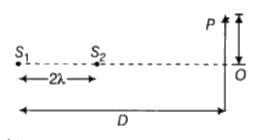 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5D
Two coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passingh through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
 View Solution
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is
 View Solution
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View Solution
